题目内容
 如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长.
如图,在梯形ABCD中,AD∥BC,∠DCB=60°,BD⊥CD,BC=6,AD=2.求AB长.考点:梯形
专题:
分析:过A,D分别作AE⊥BC,DF⊥BC,利用已知条件可求出CD长度,进而可求出DF的长,即AE的长,因为BC=6已知,所以BE可求,再利用勾股定理即可求出AB的长.
解答:解:过A,D分别作AE⊥BC,DF⊥BC,AD∥BC,
∴四边形AEFD是矩形,
∴AE=DF,AD=EF=2,
∵BD⊥CD,BC=6,∠DCB=60°,
∴DC=3,
∴DF=AE=
,CF=1.5
∴BE=BC-EF-CF=2.5,
∴AB=
=
.
∴四边形AEFD是矩形,
∴AE=DF,AD=EF=2,

∵BD⊥CD,BC=6,∠DCB=60°,
∴DC=3,
∴DF=AE=
3
| ||
| 2 |
∴BE=BC-EF-CF=2.5,
∴AB=
| AE2+BE2 |
| 13 |
点评:本题考查了梯形的性质、直角三角形的性质、勾股定理的运用以及矩形的判定和性质,题目的综合性较强,是中考常见题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
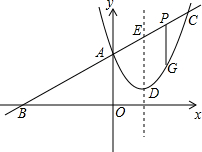 如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足
如图,已知二次函数图象的顶点坐标为D(1,1),直线y=kx+m的图象与该二次函数的图象交于A、C两点,且A(0,2),直线与x轴的交点为B,满足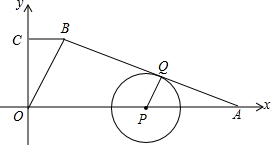 如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x,
如图,在平面直角坐标系中,已知直角梯形OABC,BC∥OA,A(21,0),C(0,8),OB=10,点P在线段AO上运动,以点P为圆心作⊙P,使⊙P始终与AB边相切,切点为Q,设⊙P的半径为8x, 如图,O为矩形ABCD的中心,M为BC边上任一点,ON⊥OM且与CD边交于点N.若AB=6,AD=4.设OM=x,ON=y,则y与x之间的函数关系式为
如图,O为矩形ABCD的中心,M为BC边上任一点,ON⊥OM且与CD边交于点N.若AB=6,AD=4.设OM=x,ON=y,则y与x之间的函数关系式为