题目内容
11.(1)先化简,再求值:($\frac{b}{a+b}$+$\frac{b}{a-b}$)÷$\frac{a}{{a}^{2}-{b}^{2}}$.其中a=2016,b=$\sqrt{2}$(2)计算:-$\sqrt{27}$+$|{\sqrt{3}-2}$|-${(\frac{1}{3})^{-1}}$+2cos60°.
分析 (1)首先进行通分,进而化简,再将已知代入求出答案;
(2)直接利用负整数指数幂的性质以及绝对值的性质、特殊角的三角函数值分别化简求出答案.
解答 解:(1)($\frac{b}{a+b}$+$\frac{b}{a-b}$)÷$\frac{a}{{a}^{2}-{b}^{2}}$
=[$\frac{b(a-b)}{(a+b)(a-b)}$+$\frac{b(a+b)}{(a+b)(a-b)}$]×$\frac{(a+b)(a-b)}{a}$
=$\frac{2ab}{(a+b)(a-b)}$×$\frac{(a+b)(a-b)}{a}$
=2b
把b=$\sqrt{2}$代入得:原式=2$\sqrt{2}$;
(2)-$\sqrt{27}$+$|{\sqrt{3}-2}$|-${(\frac{1}{3})^{-1}}$+2cos60°
=-3$\sqrt{3}$+2-$\sqrt{3}$-3+2×$\frac{\sqrt{3}}{2}$
=-2$\sqrt{3}$-1.
点评 此题主要考查了实数运算以及分式的化简求值,正确化简各数以及掌握分式的基本运算法则是解题关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
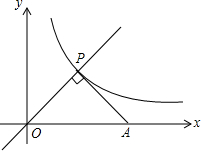 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的交点,PA⊥OP,交x轴于点A,OA=6,则k的值是9.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的交点,PA⊥OP,交x轴于点A,OA=6,则k的值是9.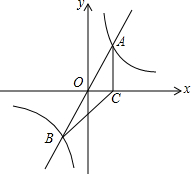 如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,正比例函数y=mx的图象与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.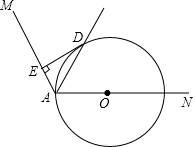 如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E.
如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E. 小猫在如图所示的地板上自由走动,并随意停留在某块方砖上,那么它停留在黑色区域上的概率是多少?
小猫在如图所示的地板上自由走动,并随意停留在某块方砖上,那么它停留在黑色区域上的概率是多少?