题目内容
16.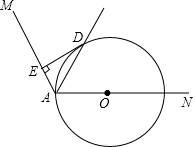 如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E.
如图,O是∠MAN的边AN上一点,以OA为半径作⊙O,交∠MAN的平分线于点D,DE⊥AM于E.(1)求证:DE是⊙O的切线;
(2)连接OE,若∠EDA=30°,AE=1,求OE的长.
分析 (1)连接OD,欲证DE是⊙O的切线,只需证明OD⊥DE即可;
(2)由∠EDA=30°,AE=1,易得AD=2,DE=$\sqrt{3}$,∠ADO=60°,进一步得出△ADO为等边三角形,得出OD=2,然后根据勾股定理即可求得OE.
解答  (1)证明:连接OD.
(1)证明:连接OD.
∵AD平分∠MAN,
∴∠EAD=∠OAD.
∵OA=OD,
∴∠ODA=∠OAD.
∴∠EAD=∠ODA.
∵DE⊥AM于E,
∴∠AED=90°.
∴∠EAD+∠EDA=90°,
∴∠ODA+∠EDA=90°.
∴OD⊥ED.
∴DE是⊙O的切线.
(2)解:∵∠EDA=30°,
∴∠ODA=60°.
∵OA=OD,
∴△ADO为等边三角形.
在Rt△AED中,AE=1,可得AD=2,$ED=\sqrt{3}$.
∴OD=AD=2.
在Rt△ODE中,由勾股定理可得$OE=\sqrt{7}$.
点评 本题考查了切线的判定与性质、勾股定理、等边三角形的判定和性质等知识点.

练习册系列答案
相关题目
6.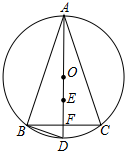 已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
 已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )
已知AD为△ABC的外接圆⊙O的直径,点E是△ABC的内心,AE的延长线交BC于点F,交⊙O于点D,BC=6,cos∠BAC=$\frac{4}{5}$,则EF的长是( )| A. | 1 | B. | 4-$\sqrt{10}$ | C. | 5-$\sqrt{10}$ | D. | $\sqrt{10}$-1 |
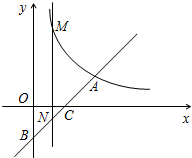 如图,在第一象限内,一次函数y=k1x-2的图象与反比例函数y=$\frac{k_2}{x}$的图象相交于点A(4,a),与y轴、x轴分别相交于B,C两点,且BC=CA.
如图,在第一象限内,一次函数y=k1x-2的图象与反比例函数y=$\frac{k_2}{x}$的图象相交于点A(4,a),与y轴、x轴分别相交于B,C两点,且BC=CA. 甲、乙两班离A地的距离分别为y1km,y2km,y1,y2与x(h)之间的函数关系如图所示,根据图象解答下列问题:
甲、乙两班离A地的距离分别为y1km,y2km,y1,y2与x(h)之间的函数关系如图所示,根据图象解答下列问题: