Question

6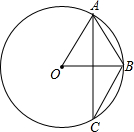．如图，A，B，C是⊙O上的三点，AB=6，∠ACB=30°，那么⊙O的半径等于6．

Answer 1

分析 根据圆周角定理求得∠AOB=2∠ACB=60°，然后由等腰三角形AOB的性质及三角形内角和定理求得∠OBA=∠OAB=∠AOB=60°；最后根据等边三角形的判定定理知△AOB是等边三角形，所以等边三角形的三条边相等．

解答 解：∵A，B，C是⊙O上的三点，∠ACB=30°，
∴∠AOB=2∠ACB=60°（同弧所对的圆周角是所对的圆心角的一半）；
 在△AOB中，OA=OB（⊙O的半径），
∴∠OBA=∠OAB，
∴∠OBA=∠OAB=60°（三角形内角和定理），
∴∠OBA=∠OAB=∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=6．
故答案为：6．

点评 本题考查了圆周角定理和等边三角形的判定与性质．解答该题时，利用圆周角定理要注意圆心角与圆周角的定义，只有三个点都在圆上所组成的角才称之为圆周角．