题目内容
15. 已知△ABC中,中线AD、BE、CF交于G点,求证:AG=2GD.
已知△ABC中,中线AD、BE、CF交于G点,求证:AG=2GD.
分析 作DH∥CF,根据三角形中位线定理可知BH=HF,由题意得AF=2FH,根据平行线分线段成比例得到比例式,计算即可.
解答 证明: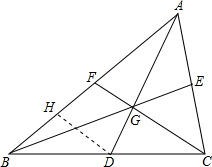 作DH∥CF交AB于H,
作DH∥CF交AB于H,
∵DH∥CF,BD=DC,
∴BH=HF,又AF=BF,
∴AF=2FH,又DH∥CF,
∴$\frac{AG}{GD}$=$\frac{AF}{FH}$,
∴AG=2GD.
点评 本题考查的是三角形的重心的概念和三角形中位线定理,正确作出辅助线、灵活运用三角形中位线定理是解题的关键.

练习册系列答案
相关题目
3.在平面直角坐标系中,抛物线y=a(x-2)2+k与x轴交于A,C两点,顶点为B,点D在抛物线的对称轴上,若四边形ABCD是一个内角为60°且边长为6的菱形,则该抛物线的解析析式有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.用三个不同的正多边形能铺满地面的是( )
| A. | 正三角形、正方形、正五边形 | B. | 正三角形、正方形、正六边形 | ||
| C. | 正三角形、正方形、正七边形 | D. | 正三角形、正方形、正八边形 |

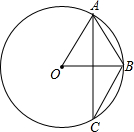 如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.
如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.