题目内容
11.若$\sqrt{12}$的整数部分为a,小数部分为b,则$\frac{2b}{a+b}$的值等于( )| A. | 2+$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 4$\sqrt{3}$-6 | D. | 4$\sqrt{3}$+6 |
分析 估算出$\sqrt{12}$的大小,从而得到a、b的值,然后代入数值进行计算即可.
解答 解:∵9<12<16,
∴3<$\sqrt{12}$<4.
∴a=3,b=$\sqrt{12}-3$=$2\sqrt{3}-3$.
∴原式=$\frac{2×(2\sqrt{3}-3)}{3+2\sqrt{3}-3}$=$\frac{4\sqrt{3}-6}{2\sqrt{3}}$=2-$\sqrt{3}$.
故选:B.
点评 本题主要考查的是估算无理数的大小,二次根式的化简,求得a、b的值是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
19.已知下列四组线段,其中能构成直角三角形的是( )
| A. | 5,12,13 | B. | 0.2,0.3,0.5 | C. | 2,3,4 | D. | $\frac{7}{4}$,1,$\frac{3}{4}$ |
3.在平面直角坐标系中,抛物线y=a(x-2)2+k与x轴交于A,C两点,顶点为B,点D在抛物线的对称轴上,若四边形ABCD是一个内角为60°且边长为6的菱形,则该抛物线的解析析式有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
1.小明的身高为1.8米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树下部分在地面上的影长为6米,上部分在竖直的墙上的影长1米,则这棵树的高为( )
| A. | 4.2米 | B. | 5.8米 | C. | 6.4米 | D. | 6.6米 |
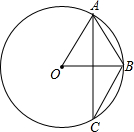 如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.
如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.