题目内容
16.若|2x-1|+|3y-4|=0,则x+y=$\frac{11}{6}$.分析 根据绝对值的和等于零,可得每个绝对值同时等于零,可得x、y的值,根据有理数的加法,可得答案.
解答 解:由|2x-1|+|3y-4|=0,得
$\left\{\begin{array}{l}{2x-1=0}\\{3y-4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{4}{3}}\end{array}\right.$,
x+y=$\frac{1}{2}$+$\frac{4}{3}$=$\frac{3}{6}$+$\frac{8}{6}$=$\frac{11}{6}$,
故答案为:$\frac{11}{6}$
点评 本题考查了非负数的性质,利用绝对值的和等于零得出x、y的值是解题关键.

练习册系列答案
相关题目
7.用三个不同的正多边形能铺满地面的是( )
| A. | 正三角形、正方形、正五边形 | B. | 正三角形、正方形、正六边形 | ||
| C. | 正三角形、正方形、正七边形 | D. | 正三角形、正方形、正八边形 |
1.小明的身高为1.8米,某一时刻他在阳光下的影长为2米,与他邻近的一棵树下部分在地面上的影长为6米,上部分在竖直的墙上的影长1米,则这棵树的高为( )
| A. | 4.2米 | B. | 5.8米 | C. | 6.4米 | D. | 6.6米 |
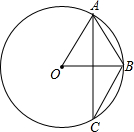 如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.
如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.