题目内容
18.$\left\{\begin{array}{l}\frac{x-3}{2}+3≥x+1\\ 1-3(x-1)<8-x\end{array}\right.$.分析 先求出每个不等式的解集,再求出不等式组的解集,即可求出答案.
解答 解:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$
∵解不等式①得:x≤1,
解不等式②得:x>-2,
∴不等式组的解集为-2<x≤1.
点评 本题考查了解一元一次不等式(组)的应用,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
相关题目
9.若分式$\frac{x-5}{2-x}$的值为2,则x的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | -3 |
3.在平面直角坐标系中,抛物线y=a(x-2)2+k与x轴交于A,C两点,顶点为B,点D在抛物线的对称轴上,若四边形ABCD是一个内角为60°且边长为6的菱形,则该抛物线的解析析式有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.用三个不同的正多边形能铺满地面的是( )
| A. | 正三角形、正方形、正五边形 | B. | 正三角形、正方形、正六边形 | ||
| C. | 正三角形、正方形、正七边形 | D. | 正三角形、正方形、正八边形 |
 观察下面的点阵图,探究其中的规律.摆第10个这样的“小屋子”需要59个点,写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式6n-1.
观察下面的点阵图,探究其中的规律.摆第10个这样的“小屋子”需要59个点,写出摆第n个这样的“小屋子”需要的总点数,S与n的关系式6n-1.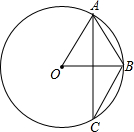 如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.
如图,A,B,C是⊙O上的三点,AB=6,∠ACB=30°,那么⊙O的半径等于6.