题目内容
14．
如图，在?ABCD中，AB=4，BC=6，∠ABC，∠BCD的角平分线分别交AD于E和F，BE与CF交于点G，则△EFG与△BCG面积之比是（ ）| A． | 2：3 | B． | 4：9 | C． | 1：4 | D． | 1：9 |
分析 由平行线和角平分线的性质可得AE=AB，DF=CD，进而求出EF的长，再由相似三角形的面积比等于对应边的平方比，即可得出结论．
解答 解：∵四边形ABCD是平行四边形，
∴AD∥BC，CD=AB=4，AD=BC=6，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AE=AB，
同理DF=CD，
∵AB=4，BC=6，
∴EF=2，
∵EF∥BC，
∴△EFG∽△BCG，
∴$\frac{{S}_{△EFG}}{{S}_{△BCG}}=（\frac{EF}{BC}）^{2}$=（$\frac{2}{6}$）2=$\frac{1}{9}$，
故选D．
点评 本题主要考查了相似三角形的判定和性质，平行四边形的性质，以及角平分线的性质等问题，能够熟练掌握各定理是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，以直线x=-1为对称轴的二次函数y=ax2+bx+c经过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a-2b+c＞0；④若（-5，y1）（$\frac{5}{2}$，y2）是该二次函数图象上的两个点，则y1＞y2．其中说法正确的是①②④．（只填序号）
9．若分式$\frac{x-5}{2-x}$的值为2，则x的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | -3 |
19．已知下列四组线段，其中能构成直角三角形的是（ ）
| A． | 5，12，13 | B． | 0.2，0.3，0.5 | C． | 2，3，4 | D． | $\frac{7}{4}$，1，$\frac{3}{4}$ |
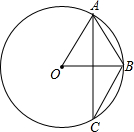如图，A，B，C是⊙O上的三点，AB=6，∠ACB=30°，那么⊙O的半径等于6．