题目内容
1．下列四个数中最大的数是（ ）| A． | 3 | B． | $\sqrt{6}$ | C． | sin60° | D． | （-2）3 |
分析 先求出sin60°=$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2\sqrt{2}}$＜$\sqrt{6}$，（-2）3=-8，再根据实数的大小比较法则比较即可．
解答 解：∵sin60°=$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{6}}{2\sqrt{2}}$＜$\sqrt{6}$，（-2）3=-8，$\sqrt{9}$=3，
∴（-2）3＜sin60°＜$\sqrt{6}$＜3，
即最大的数是3，
故选A．
点评 本题考查了特殊角的三角函数值，实数的大小比较的应用，能求出sin60°和（-2）3的值是解此题的关键．
练习册系列答案
相关题目
11．
1883年，康托尔构造的这个分形，称作康托尔集，从数轴上单位长度线段开始，康托尔取走其中间三分之一而达到第一阶段，然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段，无限地重复这一过程，余下的无穷点集就称做康托尔集，上图是康托尔集的最初几个阶段，当达到第n个阶段时，余下的所有线段的长度之和为（ ）
1883年，康托尔构造的这个分形，称作康托尔集，从数轴上单位长度线段开始，康托尔取走其中间三分之一而达到第一阶段，然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段，无限地重复这一过程，余下的无穷点集就称做康托尔集，上图是康托尔集的最初几个阶段，当达到第n个阶段时，余下的所有线段的长度之和为（ ）| A． | $\frac{2n}{3}$ | B． | $\frac{2n}{3}$ | C． | ${（\frac{2}{3}）^n}$ | D． | ${（\frac{2}{3}）^{n-1}}$ |
9．若分式$\frac{x-5}{2-x}$的值为2，则x的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | -3 |
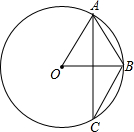如图，A，B，C是⊙O上的三点，AB=6，∠ACB=30°，那么⊙O的半径等于6．