题目内容
6.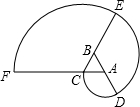 如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
分析 弧CD,弧DE,弧EF的圆心角都是120度,半径分别是1,2,3,利用弧长的计算公式可以求得三条弧长,三条弧的和就是所求曲线的长.
解答 解:弧CD的长是$\frac{120•π•1}{180}$=$\frac{2π}{3}$,
弧DE的长是:$\frac{120•π•2}{180}$=$\frac{4π}{3}$,
弧EF的长是:$\frac{120•π•3}{180}$=2π=2π,
则曲线CDEF的长是:$\frac{2π}{3}$+$\frac{4π}{3}$+2π=4π,
故答案为:4π.
点评 本题考查了弧长的计算公式,理解弧CD,弧DE,弧EF的圆心角都是120度,半径分别是1,2,3是解题的关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
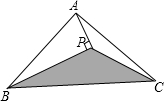 如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2.
如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2. 我们已经知道:
我们已经知道: