题目内容
18.已知实数a,b,c满足$\frac{{a}^{2}-{b}^{2}-{c}^{2}}{2bc}$+$\frac{{b}^{2}-{c}^{2}-{a}^{2}}{2ca}$+$\frac{{c}^{2}-{a}^{2}-{b}^{2}}{2ab}$=-1,求($\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$)2012+($\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ca}$)2012+($\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$)2012的值.分析 由原式可得($\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$-1)+($\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ac}$-1)+($\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$+1)=0,即$\frac{(b-c)^{2}-{a}^{2}}{2bc}$+$\frac{(a-c)^{2}-{b}^{2}}{2ac}$+$\frac{(a+b)^{2}-{c}^{2}}{2ab}$=0,利用平方差公式展开后提取公因式(啊+b-c)可得(a+b-c)($\frac{b-c-a}{2bc}$+$\frac{a-c-b}{2ac}$+$\frac{a+b+c}{2ab}$)=0,即(a+b-c)$\frac{{c}^{2}-(a-b)^{2}}{2abc}$=0,进一步分解因式即可得(a+b-c)•$\frac{(c+a-b)(c-a+b)}{2abc}$=0,从而得知a+b-c=0或c-a+b=0或c+a-b=0,继而知$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$、$\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ca}$、$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$中有两个分式的值为1,另一个为-1,即可得答案.
解答 解:由题意得$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$+$\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ac}$+$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=1,
∴($\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$-1)+($\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ac}$-1)+($\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$+1)=0,
∴$\frac{(b-c)^{2}-{a}^{2}}{2bc}$+$\frac{(a-c)^{2}-{b}^{2}}{2ac}$+$\frac{(a+b)^{2}-{c}^{2}}{2ab}$=0,
∴$\frac{(b-c-a)(b-c+a)}{2bc}$+$\frac{(a-c-b)(a-c+b)}{2ac}$+$\frac{(a+b-c)(a+b+c)}{2ab}$=0,
∴(a+b-c)($\frac{b-c-a}{2bc}$+$\frac{a-c-b}{2ac}$+$\frac{a+b+c}{2ab}$)=0,
∴(a+b-c)$\frac{ab-ac-{a}^{2}+ab-bc-{b}^{2}+ac+bc+{c}^{2}}{2abc}$=0,
∴(a+b-c)$\frac{{c}^{2}-(a-b)^{2}}{2abc}$=0,
∴(a+b-c)•$\frac{(c+a-b)(c-a+b)}{2abc}$=0,
∴a+b-c=0或c-a+b=0或c+a-b=0,
∴$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$、$\frac{{c}^{2}+{a}^{2}-{b}^{2}}{2ca}$、$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$中有两个分式的值为1,另一个为-1,
∴原式=3.
点评 本题主要考查分式的化简求值,掌握分式的运算能力是解题的根本,对已知等式变形得出a+b-c=0或c-a+b=0或c+a-b=0是解题的关键.

| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当1<x≤4时,y的取值范围是-1≤y≤3.

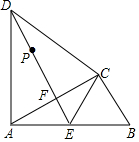 如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.
如图,在△ABC中,∠ACB=90°,以AC为底边作等腰三角形△ACD,AD=CD,E为AB的中点,连接CE、DE,DE与AC相交于点F.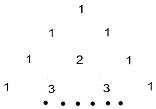 如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.
如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.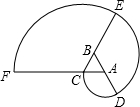 如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).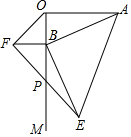 如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为2.
如图,AO⊥OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为2.
 如图,AB是⊙O的直径,C是半圆O上的一点,CD切⊙O于C,AD⊥CD,垂足为D,AD交⊙O于E,若E是$\widehat{AC}$的中点,⊙O的半径为1,则图中阴影部分的面积为$\frac{\sqrt{3}}{8}$.
如图,AB是⊙O的直径,C是半圆O上的一点,CD切⊙O于C,AD⊥CD,垂足为D,AD交⊙O于E,若E是$\widehat{AC}$的中点,⊙O的半径为1,则图中阴影部分的面积为$\frac{\sqrt{3}}{8}$.