题目内容
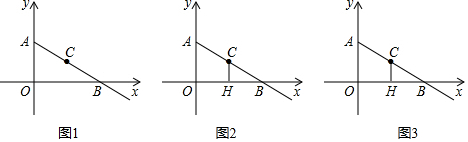
15.已知:如图,在平面直角坐标系中,射线 AB与y轴和x轴分别交于A、B 两点,点C为AB的中点,OB=$\sqrt{3}$OA=4$\sqrt{3}$,∠OAB=60°.(1)求点C的坐标;
(2)点P从点A出发以每秒2个单位的速度沿射线AB运动,由C作CH⊥OB于H,设点P运动的时间为t秒,△PCH的面积为S,用含t的式子表示S,并直接写出t的取值范围;
(3)在(2)的条件下,在射线OC上取点Q,使PQ=QH,且CQ>CH,当CQ=5时,求满足条件的t值.
分析 (1)如图1,过C作CD⊥x轴于D,过C作CE⊥y轴于E,构建平行线,得中位线CE和CD,所以得出这条线段的长,写出C的坐标;
(2)分两种情况进行讨论:①当0≤t≤2时,点P在线段AC上,如图2,分别表示PC和HQ的长,代入面积公式即可;②当2<t≤4时,点P在线段BC上,如图3,同理可求得面积S;
(3)作辅助线,构建直角三角形,根据等量关系PQ=QH,利用勾股定理列方程,解出t的值,因为动点P的总路程为8,速度为2,所以时间t的最大值为4,取舍后得出t=1.
解答 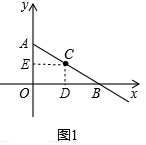 解:(1)如图1,过C作CD⊥x轴于D,过C作CE⊥y轴于E,
解:(1)如图1,过C作CD⊥x轴于D,过C作CE⊥y轴于E,
∵OB=$\sqrt{3}$OA=4$\sqrt{3}$,
∴OA=4,
∵OC⊥x轴,AO⊥x轴,
∴OC∥AO,
∵C是AB的中点,
∴E是AO的中点,
∴CE是△AOB的中位线,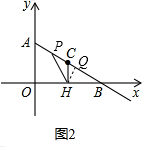
∴CE=$\frac{1}{2}$OB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
同理得:CD=$\frac{1}{2}$OA=$\frac{1}{2}$×4=2,
∴点C的坐标(2$\sqrt{3}$,2);
(2)∵OA=4,OB=4$\sqrt{3}$,
∴AB=$\sqrt{{4}^{2}+(4\sqrt{3})^{2}}$=8,
∴0≤t≤4,
分两种情况:
①当0≤t≤2时,点P在线段AC上,如图2,
∵CH⊥OB,AO⊥OB,
∴CH∥AO,
∵C是AB的中点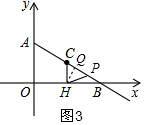 ,
,
∴H是OB的中点,
∴OH=BH=$\frac{1}{2}$OB=$\frac{1}{2}$×4$\sqrt{3}$=2$\sqrt{3}$,
过H作HQ⊥AB于Q,
∵∠OAB=60°,∠AOB=90°,
∴∠ABO=30°,
∴HQ=$\frac{1}{2}$BH=$\sqrt{3}$,
由题意得:AP=2t,则PC=AC-AP=4-2t,
∴S=$\frac{1}{2}$PC•HQ=$\frac{1}{2}$(4-2t)×$\sqrt{3}$=-$\sqrt{3}$t+2$\sqrt{3}$,
②当2<t≤4时,点P在线段BC上,如图3,
过H作HQ⊥AB于Q,
同理得HQ=$\sqrt{3}$,
∵AP=2t,
∴PC=2t-4,
∴S=$\frac{1}{2}$PC•HQ=$\frac{1}{2}$(2t-4)×$\sqrt{3}$=$\sqrt{3}$t-2$\sqrt{3}$;
(3)过P作PF⊥x轴于F,过Q作QE⊥x轴于E,作QG⊥PF,交FP的延长线于G,过P作PH⊥OA于H,得矩形HOFP和矩形GFEQ,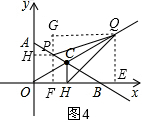
∵PH∥OB,∠ABO=30°,
∴∠APH=∠ABO=30°,
∵AP=2t,
∴AH=t,PH=$\sqrt{3}$t,
∴PF=OH=4-t,
在Rt△OQE中,∠QOE=30°,
OQ=OC+CQ=4+5=9,
∴QE=$\frac{1}{2}$OQ=$\frac{9}{2}$,
cos30°=$\frac{OE}{OQ}$,
∴OE=$\frac{\sqrt{3}}{2}$×9=$\frac{9\sqrt{3}}{2}$,
∴EH=OE-OH=$\frac{9\sqrt{3}}{2}$-2$\sqrt{3}$=$\frac{5\sqrt{3}}{2}$,
在Rt△QGP中,GQ=$\frac{9\sqrt{3}}{2}$-$\sqrt{3}$t,PG=$\frac{9}{2}$-(4-t)=$\frac{1}{2}$+t,
∵PQ=QH,
∴PG2+QG2=EH2+EQ2,
则($\frac{9\sqrt{3}}{2}$-$\sqrt{3}$t)2+($\frac{1}{2}$+t)2=($\frac{9}{2}$)2+($\frac{5\sqrt{3}}{2}$)2,
解得:t1=1,t2=$\frac{11}{2}$(舍),
则满足条件的t为1.
点评 本题是三角形的综合题,考查了30°的直角三角形的性质、中位线的性质及动点问题,掌握动点的路线、速度和时间,表示出运动的路程,根据三角形的面积公式代入可求得函数关系式,同时采用了分类讨论的方法,利用数形结合的思想解决问题.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当1<x≤4时,y的取值范围是-1≤y≤3.

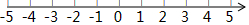 结合数轴与绝对值的知识回答下列问题:
结合数轴与绝对值的知识回答下列问题: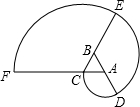 如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).
如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中$\widehat{CD}$、$\widehat{DE}$、$\widehat{EF}$圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是4π(结果保留π).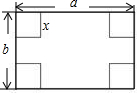 如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形,当a=12,x=3,且剪去部分的面积等于剩余部分的面积时,矩形的宽b为( )
如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形,当a=12,x=3,且剪去部分的面积等于剩余部分的面积时,矩形的宽b为( )