题目内容
16.(1)解方程:2(x-3)2=x2-9(2)已知$\frac{a}{2}$=$\frac{b}{3}$≠0,求代数式$\frac{5a-2b}{a+2b}$的值.
分析 (1)因式分解法求解可得;
(2)设$\frac{a}{2}$=$\frac{b}{3}$=k≠0,则a=2k,b=3k,代入求解可得.
解答 解:(1)∵2(x-3)2-(x+3)(x-3)=0,
∴(x-3)(x-9)=0,
则x-3=0或x-9=0,
解得:x=3或x=9;
(2)令$\frac{a}{2}$=$\frac{b}{3}$=k≠0,
则a=2k,b=3k,
∴$\frac{5a-2b}{a+2b}$=$\frac{10k-6k}{2k+6k}$=$\frac{4k}{8k}$=$\frac{1}{2}$.
点评 本题主要考查解一元二次方程的能力和比例的性质,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法和设k法求比例式的值是解题的关键.

练习册系列答案
相关题目
6.已知线段a=4,b=8,则线段a,b的比例中项为( )
| A. | ±32 | B. | 32 | C. | $±4\sqrt{2}$ | D. | $4\sqrt{2}$ |
 如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有5个.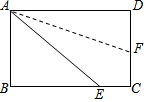 如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°..
如图,矩形ABCD沿AF折叠,使点D落在BC边上,如果∠BAE=50°,则∠DAF=20°..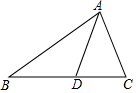 如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.
如图,D是△ABC的边BC上任一点,已知AB=4,AD=2,∠DAC=∠B,若△ABD的面积为a,则△ACD的面积为$\frac{1}{3}$a.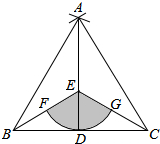 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.  如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.