题目内容
17. 如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
分析 过C作CD⊥CE与EF的延长线交于D,构成直角三角形可证出Rt△ABE∽Rt△CED,然后证出其面积;或作FH⊥CE于H,设FH=h,Rt△EHF∽Rt△BAE,然后求出其面积.
解答 解:如图,过B作BD⊥BE与EF的延长线交于D.
因为∠ACE+∠AEC=90°,∠BED+∠AEC=90°,所以∠ACE=∠BED.
于是Rt△ACE∽Rt△BED,
∴$\frac{{S}_{△BDE}}{{S}_{△EAC}}$=($\frac{BE}{AB}$)2=$\frac{1}{4}$,$\frac{BE}{BD}$=$\frac{AC}{AE}$=2,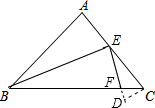
∵∠EBF=∠DBF=45°,所以BF是∠DBE的平分线,点F到BE和BD的距离相等,
∵$\frac{{S}_{△BEF}}{{S}_{△BDF}}$=$\frac{BE}{BD}$=2,
∴S△BEF=$\frac{2}{3}$S△CDE=$\frac{2}{3}$×$\frac{1}{4}$S△ACE=$\frac{2}{3}$×$\frac{1}{4}$×$\frac{1}{2}$S△ABC=$\frac{1}{6}$,
故答案为:$\frac{1}{6}$.
点评 本题考查了等腰三角形的性质,相似三角形的性质和三角形的面积公式,解题的关键是作出辅助线,然后构成直角三角形,用相似三角形的性质求面积.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
5.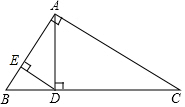 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,AD=3,DE=2,则CD的长是( )| A. | $\frac{21}{2}$ | B. | $\frac{{\sqrt{15}}}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{{3\sqrt{5}}}{2}$ |
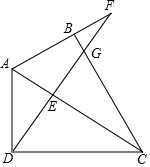 如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF. 如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?
如图,AB,CD是⊙O的两条弦,AD,CB的延长线相交于点E,DC=DE.AB和BE相等吗?为什么?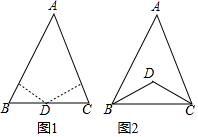 已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.
已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.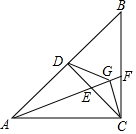 如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.
如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.