题目内容
7. 如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
如图,在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,DM=DN,过D作DF⊥AC于F,证明:AM+AN=2AF.
分析 过点D作DG⊥AB于G,由HL分别证明Rt△ADG≌Rt△ADF和Rt△DFN≌Rt△DGM,得MG=NF,AG=AF,再把AM+AN变形即可得出结论.
解答 证明:过点D作DG⊥AB于G,如图所示: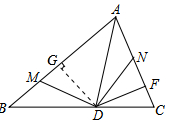
∵AD平分∠BAC,DF⊥AC,
∴DF=DG,
在Rt△ADG和Rt△ADF中,$\left\{\begin{array}{l}{DF=DG}\\{AD=AD}\end{array}\right.$,
∴Rt△ADG≌Rt△ADF(HL),
∴AG=AF,
在Rt△DFN和Rt△DGM中,$\left\{\begin{array}{l}{DF=DG}\\{DN=DM}\end{array}\right.$,
∴Rt△DFN≌Rt△DGM(HL),
∴MG=NF
又∵AG=AF,
∴AM+AN=AG+MG+AN=AF+NF+AN=2AF.
点评 本题主要考查了全等三角形的性质和判定、角平分线的性质定理等知识;熟练掌握全等直角三角形的判定与性质,并通过作辅助线构建全等三角形是解决问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
17.由二次函数y=6(x-2)2+1,可知( )
| A. | 图象的开口向下 | B. | 图象的对称轴为直线x=$\frac{3}{2}$ | ||
| C. | 函数的最大值为1 | D. | 当x>2时,y随x的增大而增大 |
18.已知线段 a=2,b=8,则 a,b 的比例中项线段为( )
| A. | 16 | B. | ±4 | C. | 4 | D. | -4 |
2.泸溪三口岩水库移民新村分给小慧家一套价格为12万元的住房,按要求,需首期(第一年)付房款3万元,从第二年起,每年应付房款0.5万元与上一年剩余房款的利息的和,假设剩余房款年利率为0.4%,小慧列表推算如下:
若第n年小慧家仍需还款,则第n年应还款0.54-0.002n万元(用含n的代数式表示,n>1).
| 第一年 | 第二年 | 第三年 | … | |
| 应还款(万元) | 3 | 0.5+9×0.4% | 0.5+8.5×0.4% | … |
| 剩余房款(万元) | 9 | 8.5 | 8 | … |
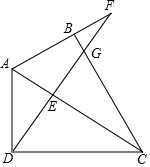 如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.