Question

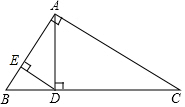
4．如图，在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD=ED；②AC+BE=AB；③∠BDE=∠BAC；④DA平分∠CDE；⑤S_△ABD：S_△ACD=AB：AC．其中，正确的有5个．

Answer 1

分析 由在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E．可得CD=DE，继而可得∠ADC=∠ADE，又由角平分线的性质，证得AE=AD，由等角的余角相等，可证得∠BDE=∠BAC，由三角形的面积公式，可证得S_△ABD：S_△ACD=AB：AC．

解答 解：∵在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于E，
∴CD=ED，
故①正确；
∴∠CDE=90°-∠BAD，∠ADC=90°-∠CAD，
∴∠ADE=∠ADC，
即AD平分∠CDE，
故④正确；
∴AE=AC，
∴AB=AE+BE=AC+BE，
故②正确；
∵∠BDE+∠B=90°，∠B+∠BAC=90°，
∴∠BDE=∠BAC，
故③正确；
∵S_△ABD=$\frac{1}{2}$AB•DE，S_△ACD=$\frac{1}{2}$AC•CD，
∵CD=ED，
∴S_△ABD：S_△ACD=AB：AC，
故⑤正确．
故答案为：①②③④⑤．

点评 此题考查了角平分线的性质以及三角形的面积问题．此题难度适中，注意掌握数形结合思想的应用．