题目内容
1．
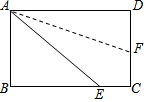如图，矩形ABCD沿AF折叠，使点D落在BC边上，如果∠BAE=50°，则∠DAF=20°．．
分析 先依据直角三角形两锐角互余求得求得∠BAE的度数，然后依据平行线的性质可求得∠EAD的度数，然后依据翻折的性质得到∠EAF=∠DAF．
解答 解：∵四边形ABCD为矩形，
∴∠B=90°，AD∥BC．
∵∠B=90°，∠BAE=50°，
∴∠AEB=40°．
∵AD∥BC，
∴∠AEB=∠EAD=40°．
由翻折的性质可知：∠EAF=∠DAF．
∴∠DAF=20°．
故答案为：20°．
点评 本题主要考查的是翻折变换、矩形的性质，熟练掌握翻折的性质是解题的关键．
练习册系列答案
相关题目
