题目内容
20.函数y=ax2+bx-1,当y>0时解为x<-0.5或x>1,则a=2,b=-1.分析 根据已知条件得出:与x轴交点为(-0.5,0)和(1,0),代入解析式列方程组解出即可.
解答 解:∵当y>0时解为x<-0.5或x>1,
∴与x轴交点为(-0.5,0)和(1,0),
把(-0.5,0)和(1,0)代入y=ax2+bx-1得:
$\left\{\begin{array}{l}{-0.25a-0.5b-1=0}\\{a+b-1=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=-1}\end{array}\right.$,
故答案为:2,-1.
点评 本题考查了利用待定系数法求二次函数的解析式,本题与其他题不同,没有直接给出抛物线上点的坐标,而是以其它形式给出条件,所以要认真理解题意,熟练掌握二次函数图象的性质.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
10.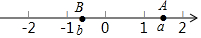 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
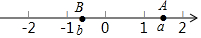 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )| A. | ab>0 | B. | b-a>0 | C. | (a-1)(b-1)>0 | D. | (a-1)(b+1)>0 |
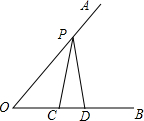 如图,∠AOB=60°,OP=12cm,OC=5cm,PC=PD,求OD的长.
如图,∠AOB=60°,OP=12cm,OC=5cm,PC=PD,求OD的长.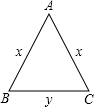 如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)
如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm)