题目内容
12.若抛物线y=x2+(m-1)x+(m+3)经过原点,则m=-3,若其顶点为y轴上,则m=1.分析 当图象过原点时,则常数项为0,当其顶点在y轴上时,则一次项系数为0,则可分别得到关于m的方程,可求得m的值.
解答 解:
当抛物线y=x2+(m-1)x+(m+3)经过原点时,
则有m+3=0,解得m=-3,
当顶点在y轴上时则有其对称轴为x=0,
∴m-1=0,解得m=1,
故答案为:-3;1.
点评 本题主要考查二次函数的性质,掌握抛物线的顶点坐标公式是解题的关键.

练习册系列答案
相关题目
2.用等式的性质解方程$\frac{1}{3}$x+5=4,求得方程的根是( )
| A. | 27 | B. | -3 | C. | 9 | D. | 3 |
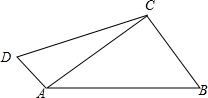 已知:如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.求证:△ACD是直角三角形.
已知:如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.求证:△ACD是直角三角形.