题目内容
20．解方程组或不等式（1）$\left\{\begin{array}{l}\frac{y+1}{4}=\frac{x+2}{3}\\ 2x-3y=1\end{array}\right.$
（2）$\frac{2x+3}{2}$-$\frac{x-2}{6}$＜4．
分析 （1）整理原方程组后利用加减消元法求解即可得；
（2）根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
解答 解：（1）原方程组整理，得：$\left\{\begin{array}{l}{4x-3y=-5}&{①}\\{2x-3y=1}&{②}\end{array}\right.$，
①-②，得：2x=-6，
解得：x=-3，
将x=-3代入①，得：-12-3y=-5，
解得：y=-$\frac{7}{3}$，
∴方程组的解为：$\left\{\begin{array}{l}{x=-3}\\{y=-\frac{7}{3}}\end{array}\right.$；
（2）去分母，得：3（2x+3）-（x-2）＜24，
去括号，得：6x+9-x+2＜24，
移项、合并同类项，得：5x＜13，
系数化为1，得：x＜$\frac{13}{5}$．
点评 本题主要考查解二元一次方程组和一元一次不等式的能力，熟练掌握解方程组的两种消元方法和解不等式得基本步骤是解题的关键．
练习册系列答案
相关题目
如图，△DEF是△ABC经过某种变换得到的图形，点A与点D，点B与点E，
8．
在平面直角坐标系中（以1cm为单位长度），过A（0，4）的直线垂直于y轴，点M（9，4）为直线上一点，若点P从点M出发，以每秒3cm的速度沿这条直线向左移动；点Q从原点同时出发，以每秒1cm的速度沿x轴向右移动，几秒后PQ平行于y轴（ ）
在平面直角坐标系中（以1cm为单位长度），过A（0，4）的直线垂直于y轴，点M（9，4）为直线上一点，若点P从点M出发，以每秒3cm的速度沿这条直线向左移动；点Q从原点同时出发，以每秒1cm的速度沿x轴向右移动，几秒后PQ平行于y轴（ ）| A． | $\frac{3}{2}$ | B． | $\frac{9}{4}$ | C． | 3 | D． | 2 |
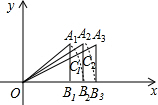如图，在平面直角坐标系中，已知A1（1，1），B1（1，0），以O为圆心OA1为半径作圆弧交x轴于B2，作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1，以O为圆心OA2为半径作圆弧交x轴于B3，作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2，…，按此规律，则Cn的纵坐标为（$\sqrt{n}$，$\frac{\sqrt{n}}{\sqrt{n+1}}$）（结果用n的代数式表示）
如图，在直角坐标系中，A（1，3），B（2，0），第一次将△AOB变换成△OA1B1，A1（2，3），B1（4，0）；第二次将△OA1B1变换成△OA2B2，A2（4，3），B2（8，0），第三次将△OA2B2变换成△OA3B3，则B2016的横坐标为22017．．