题目内容
5.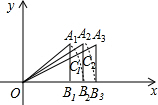 如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示)
如图,在平面直角坐标系中,已知A1(1,1),B1(1,0),以O为圆心OA1为半径作圆弧交x轴于B2,作Rt△A2B2O使得A2B2=A1B1且OA2交A1B1于C1,以O为圆心OA2为半径作圆弧交x轴于B3,作Rt△A3B3O使得A3B3=A2B2且OA3交A2B2于C2,…,按此规律,则Cn的纵坐标为($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)(结果用n的代数式表示)
分析 易证Rt△OC1 B1∽Rt△OA2 B2,所以有$\frac{{C}_{1}B}{{A}_{2}{B}_{2}}=\frac{OB1}{O{B}_{2}}$,而A2 B2=1,OB1=1,OB2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.所以C1 B1=$\frac{1×1}{\sqrt{2}}$,故:C1(1,$\frac{1}{\sqrt{2}}$)…以此类推,直至找出规律.
解答 解:由题意得:Rt△OC1 B1∽Rt△OA2 B2,
∴$\frac{{C}_{1}B}{{A}_{2}{B}_{2}}=\frac{OB1}{O{B}_{2}}$
∵A2 B2=1,OB1=1,OB2=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴C1 B1=$\frac{1×1}{\sqrt{2}}$,C1 (1,$\frac{1}{\sqrt{2}}$).
同理可得:C2 B2=$\frac{1×\sqrt{2}}{\sqrt{3}}$,C2 ($\sqrt{2}$,$\frac{1×\sqrt{2}}{\sqrt{3}}$)
C3 B3=$\frac{1×\sqrt{3}}{\sqrt{4}}$,C3 ($\sqrt{3}$,$\frac{1×\sqrt{3}}{\sqrt{4}}$)…
∴Cn ($\sqrt{n}$,$\frac{\sqrt{n}}{\sqrt{n+1}}$)
点评 本题考查了直角坐标系中点的坐标的变化规律问题,解题的关键是求出Cn Bn的长与OBn 的长.

练习册系列答案
相关题目
13.某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如表:
上表反映了两 个变量之间的关系,其中,自变量是香蕉数量;因变量是售价.
| 数量(千克) | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
| 售价(元) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 | 10.5 | … |
15. 某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求被调查的家庭中,用水量不超过15吨的家庭占总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
 某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:
某中学九(2)班同学为了了解2014年某小区家庭月均用水情况,随机调查了该小区的部分家庭,并将调查数据进行如下整理:| 月均用水量x(吨) | 频数 | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | 12 | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | 0.08 |
| 25<x≤3 | 2 | 0.04 |
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)求被调查的家庭中,用水量不超过15吨的家庭占总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20吨的家庭大约有多少户?
 如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积.
如图,圆锥的底面半径是2cm,当圆锥的高由小到大变化时,圆锥的体积也随之发生了变化.在这个变化过程中,自变量是圆锥的高,因变量是圆锥的体积. 如图所示,是反映了爷爷每天晚饭后从家中出发去散步的时间与距离之间的关系的一幅图.
如图所示,是反映了爷爷每天晚饭后从家中出发去散步的时间与距离之间的关系的一幅图.