题目内容
 已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.
已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.(1)请说明△ABC是等边三角形;
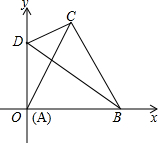
(2)以点A为坐标原点,AB所在直线为x轴建立如图所示平面直角坐标系,D是y轴上一点,连接DB、DC,∠ODB=60°,猜想线段DO、DC、DB之间有何数量关系?并证明你的结论.
考点:全等三角形的判定与性质,非负数的性质:偶次方,等边三角形的判定与性质
专题:
分析:(1)根据(a-b)2+b2-2bc+c2=0,即可求得a=b=c,即可判定△ABC是等边三角形;
(2)在BD上找到点F使DF=OD,连接OF,可得△ODF是等边三角形,易证△DOC≌△FOB,可得BF=CD,即可求得BD=OD+CD.
(2)在BD上找到点F使DF=OD,连接OF,可得△ODF是等边三角形,易证△DOC≌△FOB,可得BF=CD,即可求得BD=OD+CD.
解答:解:(1)∵(a-b)2+b2-2bc+c2=0,
∴(a-b)2+(b-c)2=0,
∵(a-b)2≥0,(b-c)2≥0,
∴a=b=c,
∴△ABC是等边三角形;
(2)在BD上找到点F使DF=OD,连接OF,
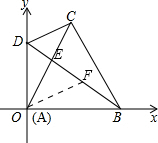
∵∠ODB=60°,OD=DF,
∴△ODF是等边三角形;
∴OF=OD,
∵∠DOF=∠COB=60°,
∴∠DOC=∠FOB,
在△DOC和△FOB中,
,
∴△DOC≌△FOB(SAS),
∴BF=CD,
∴BD=DF+BF=OD+CD.
∴(a-b)2+(b-c)2=0,
∵(a-b)2≥0,(b-c)2≥0,
∴a=b=c,
∴△ABC是等边三角形;
(2)在BD上找到点F使DF=OD,连接OF,

∵∠ODB=60°,OD=DF,
∴△ODF是等边三角形;
∴OF=OD,
∵∠DOF=∠COB=60°,
∴∠DOC=∠FOB,
在△DOC和△FOB中,
|
∴△DOC≌△FOB(SAS),
∴BF=CD,
∴BD=DF+BF=OD+CD.
点评:本题考查了全等三角形的判定,考查了等边三角形边长相等性质,考查了全等三角形对应边相等的性质,本题中求证△DOC≌△FOB是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
下列说法不成立的是( )
| A、若两图形关于某直线对称,那么对称轴是对应点连线的中垂线 |
| B、两图形若关于某直线对称,则两图形能重合 |
| C、等腰三角形是轴对称图形 |
| D、线段的对称轴只有一条 |
 如图,已知矩形ABCD∽矩形ECDF,且AB=BE,那么BC与AB的比值是( )
如图,已知矩形ABCD∽矩形ECDF,且AB=BE,那么BC与AB的比值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
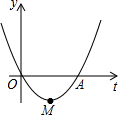 如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.
如图,抛物线y=x2+bx+c过原点,且与x轴交于A(4,0),M为抛物线的顶点,问抛物线是否存在点P,使得∠POM=90°?若存在,求出点P坐标;若不存在,说明理由.
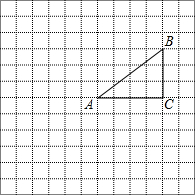 如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点.
如图,正方形网格中每个小正方形的边长都是1,△ABC的三个顶点A、B、C都是格点. 如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )
如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )