题目内容
已知⊙O的直径为5,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.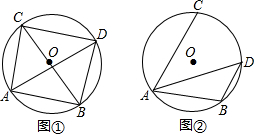
(Ⅰ)如图①,若BC为⊙O的直径,AB=3,则AC= ,BD= ;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.

(Ⅰ)如图①,若BC为⊙O的直径,AB=3,则AC=
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
考点:圆周角定理,勾股定理
专题:
分析:(1)BC为直径可知△ABC为直角三角形,利用勾股定理可求得AC,再结合AD为角平分线,可得CD=BD,在Rt△CBD中可求得BD;
(2)连接OB、OD,则可知∠BOD=2∠DAB=∠CAB=60°,可知△BOD为等边三角形,可知BD=OB,可求得BD的长.
(2)连接OB、OD,则可知∠BOD=2∠DAB=∠CAB=60°,可知△BOD为等边三角形,可知BD=OB,可求得BD的长.
解答:解:
(1)∵BC为直径,
∴∠CAB=∠CDB=90°,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴CD=BD,
在Rt△ABC中,BC=5,AB=3,由勾股定理可求得AC=4,
在Rt△CBD中,BC=5,CD=BD,由勾股定理可求得BD=
,
故答案为:4;
;
(2)如图,连接OB、OD,
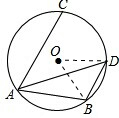
∵AD平分∠CAB,
∴∠CAD=∠BAD=30°,
∴∠BOD=2∠BAD=60°,且OB=OD,
∴△BOD为等边三角形,
∴BD=OB,
又直径为5,
∴BD=2.5.
(1)∵BC为直径,
∴∠CAB=∠CDB=90°,
∵AD平分∠CAB,
∴∠CAD=∠BAD,
∴CD=BD,
在Rt△ABC中,BC=5,AB=3,由勾股定理可求得AC=4,
在Rt△CBD中,BC=5,CD=BD,由勾股定理可求得BD=
5
| ||
| 2 |
故答案为:4;
5
| ||
| 2 |
(2)如图,连接OB、OD,

∵AD平分∠CAB,
∴∠CAD=∠BAD=30°,
∴∠BOD=2∠BAD=60°,且OB=OD,
∴△BOD为等边三角形,
∴BD=OB,
又直径为5,
∴BD=2.5.
点评:本题主要考查圆周角定理及等边三角形的判定和性质,掌握在同圆或等圆中相等的圆周角所对的弦相等是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
抛物线y=x2-2x-1的对称轴是( )
| A、x=1 | B、x=-1 |
| C、x=2 | D、x=-2 |
 已知?ABCD的周长为28cm,对角线AC、BD相交于点O,且△OAB的周长比△OBC的周长大4cm,且∠A=30°,求?ABCD的面积.
已知?ABCD的周长为28cm,对角线AC、BD相交于点O,且△OAB的周长比△OBC的周长大4cm,且∠A=30°,求?ABCD的面积.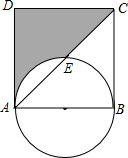 如图,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E.
如图,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E.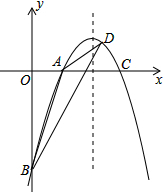 如图,已知二次函数y=
如图,已知二次函数y=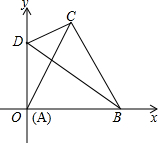 已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.
已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.