题目内容
抛物线y=（2x-4）2-3的对称轴为直线 ．
考点：二次函数的性质
专题：
分析：先将y=（2x-4）2-3变形为y=4（x-2）2-3，再根据顶点式解析式确定对称轴即可．
解答：解：∵y=（2x-4）2-3=4（x-2）2-3，
∴抛物线的对称轴为直线x=2．
故答案为：x=2．
∴抛物线的对称轴为直线x=2．
故答案为：x=2．
点评：本题考查了二次函数的性质．抛物线y=a（x-h）2+k的顶点坐标为（h，k），对称轴为x=h．
练习册系列答案
提分百分百检测卷系列答案
相关题目
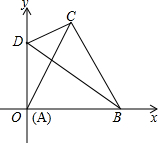
如图，在四边形ABCD中，边AB与AD关于AC对称，则下面结论正确的是（ ）①CA平分∠BCD；②AC平分∠BAD；③DB⊥AC；④BE=DE．
| A、② | B、①② |
| C、②③④ | D、①②③④ |
已知a、b、c为△ABC的三边，且满足（a-b）2+b2-2bc+c2=0．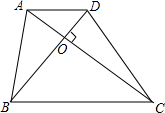
如图所示已知梯形ABCD中，AD∥BC，BD=6，AC=8，AC⊥BD于O，