Question

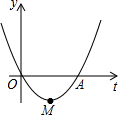如图，抛物线y=x²+bx+c过原点，且与x轴交于A（4，0），M为抛物线的顶点，问抛物线是否存在点P，使得∠POM=90°？若存在，求出点P坐标；若不存在，说明理由．

Answer 1

考点：二次函数的性质

专题：

分析：先将A（4，0），O（0，0）代入y=x²+bx+c，列方程组求b、c的值，确定抛物线解析式，用配方法求出顶点M的坐标，再设P（m，m²-4m），过P作PE⊥y轴，垂足为E；过M点作MF⊥y轴，垂足为F，利用互余关系证明∠EPO=∠FOM，可证Rt△OEP∽Rt△MFO，利用相似比求m的值即可．

解答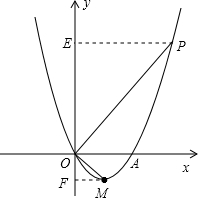：解：将A（4，0），O（0，0）代入y=x²+bx+c，
得

16+4b+c=0 c=0

，解得

b=-4 c=0

，
所以y=x²-4x，即y=（x-2）²-4，
顶点M（2，-4）．
设抛物线上存在一点P，使OP⊥OM，其坐标为（m，m²-4m），
过P作PE⊥y轴，垂足为E；过M点作MF⊥y轴，垂足为F．
∵∠POE+∠MOF=90°，∠POE+∠EPO=90°，
∴∠EPO=∠FOM．
在△OEP与△MFO中，

∠OEP=∠MFO=90° ∠EPO=∠FOM

，
∴△OEP∽△MFO，
∴OE：MF=EP：OF，即（m²-4m）：2=m：4，
解得m₁=0（舍去），m₂=

9

2

．
故抛物线上存在一点P，使∠POM=90°，P点的坐标为（

9

2

，

9

4

）．

点评：本题考查了二次函数的性质．关键是根据已知点的坐标求抛物线解析式，根据∠POM=90°构造相似三角形，利用相似比求解．