题目内容
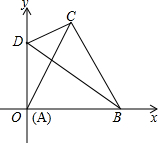
 如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )
如图所示,菱形ABCD中,对角线AC、BC相交于点O,H为AD边中点,菱形ABCD的周长为16,则OH的长等于( )| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
考点:菱形的性质
专题:
分析:根据菱形的四条边都相等求出AB,再根据菱形的对角线互相平分可得OB=OD,然后求出OH是△ABD的中位线,根据三角形的中位线平行于第三边并且等于第三边的一半求解即可.
解答:解:∵菱形ABCD的周长为16,
∴AB=16÷4=4,
∵对角线AC、BC相交于点O,
∴OB=OD,
又∵H为AD边中点,
∴OH是△ABD的中位线,
∴OH=
AB=
×4=2.
故选C.
∴AB=16÷4=4,
∵对角线AC、BC相交于点O,
∴OB=OD,
又∵H为AD边中点,
∴OH是△ABD的中位线,
∴OH=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查了菱形的性质,三角形的中位线平行于第三边并且等于第三边的一半,熟记性质并求出OH是△ABD的中位线是解题的关键.

练习册系列答案
相关题目
下列标志中,可以看作是中心对称图形有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
 已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.
已知a、b、c为△ABC的三边,且满足(a-b)2+b2-2bc+c2=0.