题目内容
13.计算(1)$\sqrt{12}+\sqrt{27}+\sqrt{18}-\sqrt{32}$
(2)$2\sqrt{12}×\frac{{\sqrt{3}}}{4}÷5\sqrt{2}$
(3)$(2\sqrt{48}-3\sqrt{27})÷\sqrt{6}$
(4)$\sqrt{\frac{2}{3}}-(\frac{1}{6}\sqrt{24}-\frac{3}{2}\sqrt{12})+(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据二次根式的乘除法则运算;
(3)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(4)先把各二次根式化为最简二次根式,再利用平方差公式计算,然后合并即可.
解答 解:(1)原式=2$\sqrt{3}$+3$\sqrt{3}$+3$\sqrt{2}$-4$\sqrt{2}$
=5$\sqrt{3}$-$\sqrt{2}$;
(2)原式=2×$\frac{1}{4}$×$\sqrt{12×3×\frac{1}{2}}$
=$\frac{3\sqrt{2}}{2}$;
(3)原式=(6$\sqrt{3}$-9$\sqrt{3}$)÷$\sqrt{6}$
=-3$\sqrt{3}$÷$\sqrt{6}$
=-$\frac{3\sqrt{2}}{2}$;
(4)原式=$\frac{\sqrt{6}}{3}$-$\frac{\sqrt{6}}{3}$+3$\sqrt{3}$+3-2
=3$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
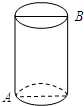 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为6$\sqrt{5}$cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为6$\sqrt{5}$cm(π取3.0).