题目内容
5．
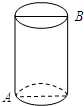如图所示，有一个圆柱体，高为12cm，底面半径为3cm，在圆柱下底面A处有一只蜘蛛．它想到上底面B处捉住一只苍蝇，则蜘蛛所走的最短路线长应为6$\sqrt{5}$cm（π取3.0）．
分析 要求需要爬行的最短路径首先要把圆柱的侧面积展开，得到一个矩形，然后利用勾股定理求两点间的线段即可．
解答 
解：如图，把圆柱的侧面展开，得到如图所示的图形，
其中AC=6cm，BC=12cm，
在Rt△ABC中，AB=$\sqrt{{6}^{2}+1{2}^{2}}$=6$\sqrt{5}$cm．
故答案为：6$\sqrt{5}$．
点评 本题考查了平面展开-最短路径问题，解题的关键是理解要求需要爬行的最短路径首先要把圆柱的侧面积展开，底面周长和高以及所走的路线构成一个直角三角形，然后再求线段的长．
练习册系列答案
相关题目
如图，在直角坐标系中有A（-2，8），B（-11，6），（-14，0），D（0，0）．
20．下列说法正确的是（ ）
| A． | 有且只有一条直线与已知直线垂直 | |
| B． | 经过一点有且只有一条直线与已知直线垂直 | |
| C． | 过点A作直线m的垂线段，则这条垂线段叫做点A到直线m的距离 | |
| D． | 连结两点的线段叫做这两点间的距离 |
10．已知：2m=1，2n=3，则2m+2n=（ ）
| A． | 9 | B． | 8 | C． | 7 | D． | 6 |
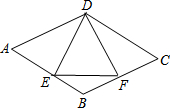如图，已知菱形ABCD中，E是AB的中点，且DE⊥AB于E，设AB=a．求：
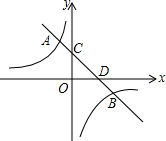如图，反比例函数y=$\frac{k}{x}$与一次函数y=kx-k+2在同一直角坐标系中的图象相交于A，B两点，其中A（-1，3），直线y=kx-k+2与坐标轴分别交于C，D两点，下列说法：①k＜0；②点B的坐标为（3，-1）；③当x＜-1时，$\frac{k}{x}$＜kx-k+2；④tan∠OCD=-$\frac{1}{k}$，其中正确的是（ ）