题目内容
8.已知x-2y=0(x≠0),求$\frac{{{x^2}-{y^2}}}{{{x^2}-2xy+{y^2}}}•\frac{x+3y}{x+y}$的值.分析 原式约分得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:∵x-2y=0,即x=2y,
∴原式=$\frac{(x+y)(x-y)}{(x-y)^{2}}$•$\frac{x+3y}{x+y}$=$\frac{x+3y}{x-y}$=$\frac{2y+3y}{2y-y}$=5.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
20.下列说法正确的是( )
| A. | 有且只有一条直线与已知直线垂直 | |
| B. | 经过一点有且只有一条直线与已知直线垂直 | |
| C. | 过点A作直线m的垂线段,则这条垂线段叫做点A到直线m的距离 | |
| D. | 连结两点的线段叫做这两点间的距离 |
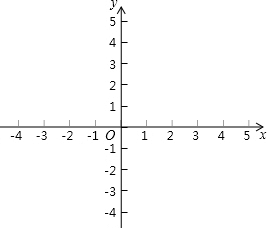 如图,在直角坐标系中有A(-2,8),B(-11,6),(-14,0),D(0,0).
如图,在直角坐标系中有A(-2,8),B(-11,6),(-14,0),D(0,0).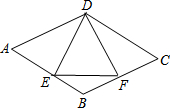 如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB于E,设AB=a.求:
如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB于E,设AB=a.求: