题目内容
9.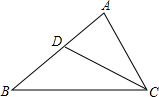 已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.
已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.
分析 在CB上截取CE=CA,连接DE,先证出BE=AD,再由SAS证明△CDE≌△CDA,得出ED=AD,∠DEC=∠A,因此BE=ED,得出∠B=∠BDE,由三角形外角的性质得出∠DEC=∠B+∠BDE,即可得出结论.
解答 证明:在CB上截取CE=CA,连接DE,如图所示: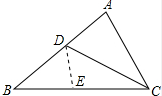 ∵BC=AC+AD,
∵BC=AC+AD,
∴BE=AD,
∵CD平分∠ACB,
∴∠DCE=∠DCA,
在△CDE和△CDA中,$\left\{\begin{array}{l}{CE=CA}&{\;}\\{∠DCE=∠DCA}&{\;}\\{CD=CD}&{\;}\end{array}\right.$,
∴△CDE≌△CDA(SAS),
∴ED=AD,∠DEC=∠A,
∴BE=ED,
∴∠B=∠BDE,
∵∠DEC=∠B+∠BDE,
∴∠A=2∠B.
点评 本题考查了等腰三角形的判定与性质、全等三角形的判定与性质、三角形的外角性质;本题有一定难度,需要通过作辅助线构造三角形全等才能得出结论.

练习册系列答案
相关题目
18. 用一个平面去截一个圆柱体,截面不可能的是( )
用一个平面去截一个圆柱体,截面不可能的是( )
 用一个平面去截一个圆柱体,截面不可能的是( )
用一个平面去截一个圆柱体,截面不可能的是( )| A. |  | B. |  | C. |  | D. |  |
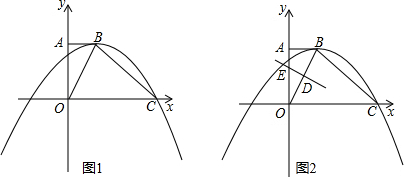
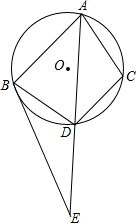 △ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
△ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.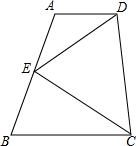 如图,在梯形ABCD中,AD∥BC,E是AB的中点.
如图,在梯形ABCD中,AD∥BC,E是AB的中点.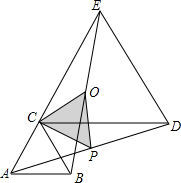 如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.
如图,△ABC和△CDE都是等边三角形,P是线段AD的中点,Q是线段BE的中点.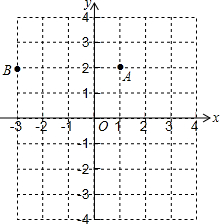 在平面直角坐标系中,A、B点的位置如图所示,
在平面直角坐标系中,A、B点的位置如图所示,