题目内容
19.在一次数学活动课上,老师带领学生去测一条南北流向的河宽(把河两岸看做平行线),某同学在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°方向上.(1)请根据题意画出示意图;
(2)请计算出这条河的宽度(参考数值:tan31°≈$\frac{3}{5}$,sin31°≈$\frac{1}{2}$).
分析 (1)根据方向角的定义及已知条件即可画出示意图;
(2)过点C作CD⊥AB于D,由题意知道∠DAC=31°,∠DBC=45°,设CD=x米,则AD=AB+BD=(20+x)米,在Rt△ACD中,tan∠DAC=$\frac{CD}{AD}$,由此可以列出关于x的方程,解方程即可求解.
解答 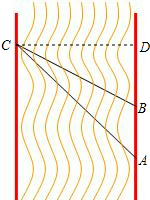 解:(1)如图所示:
解:(1)如图所示:
(2)过点C作CD⊥AB,垂足为D,设CD=x米,
∵在Rt△BCD中,∠CBD=45°,
∴BD=CD=x米.
在Rt△ACD中,∠DAC=31°,
AD=AB+BD=(20+x)米,CD=x米,
∵tan∠DAC=$\frac{CD}{AD}$,
∴$\frac{x}{20+x}$=$\frac{3}{5}$,
解得x=30.
经检验x=30是原方程的解,且符合题意.
答:这条河的宽度为30米.
点评 此题主要考查了解直角三角形-方向角问题,解题时首先正确理解题意,然后根据题目隐含的数量关系列出方程解决问题.

练习册系列答案
相关题目
10.菱形ABCD的对角线长分别为6和8,则菱形的面积为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
8.已知直线m∥n,点A在m上,点B、C、D在n上,且AB=4cm,AC=5cm,AD=6cm,则m与n之间的距离( )
| A. | 等于5cm | B. | 等于6cm | C. | 等于4cm | D. | 小于或等于4cm |
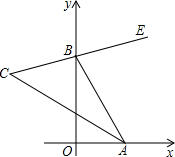 已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.
已知如图∠xOy=90°,BE是∠ABy的平分线,BE的反向延长线与∠OAB的平分线相交于点C,当点A,B分别在射线Ox,Oy上移动时,试问∠ACB的大小是否发生变化?如果保持不变,请说明理由;如果随点A,B的移动而变化,请求出变化范围.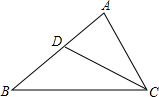 已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.
已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.