题目内容
17.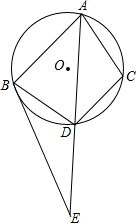 △ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
△ABC内接于⊙O,BE与⊙O相切于点B,D是⊙O上的一点,AD的延长线交BE于点E,AB•BE=AE•DC,求证:BD是∠CBE的平分线.
分析 连接BC,由BE与⊙O相切于点B,得到∠1=∠2,证得△ABE∽△EDB,得到比例式$\frac{AB}{BD}=\frac{AE}{BE}$,由于AB•BE=AE•DC,得到比例式$\frac{AB}{CD}=\frac{AE}{BE}$,于是BD=CD,证得∠2=∠3,通过等量代换可得BD是∠CBE的平分线.
解答 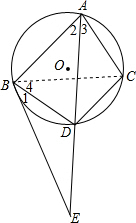 证明:连接BC,
证明:连接BC,
∵BE与⊙O相切于点B,
∴∠1=∠2,
∵∠E=∠E,
∴△ABE∽△EDB,
∴$\frac{AB}{BD}=\frac{AE}{BE}$,
∵AB•BE=AE•DC,
∴$\frac{AB}{CD}=\frac{AE}{BE}$,
∴$\frac{AB}{BD}=\frac{AB}{CD}$,
∴BD=CD,
∴$\widehat{BD}=\widehat{CD}$,
∴∠2=∠3,
∵∠3=∠4,
∴∠1=∠4,
∴BD是∠CBE的平分线.
点评 本题考查了切线的性质,相似三角形的判定和性质,弦切角定理,圆周角定理,掌握定理是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
8.已知直线m∥n,点A在m上,点B、C、D在n上,且AB=4cm,AC=5cm,AD=6cm,则m与n之间的距离( )
| A. | 等于5cm | B. | 等于6cm | C. | 等于4cm | D. | 小于或等于4cm |
6. 如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )
如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )
 如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )
如图,在2×2正方形网格中,△ABC是以格点为顶点的三角形,则sin∠CAB=( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3}{10}$ |
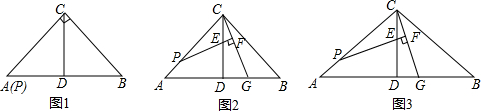
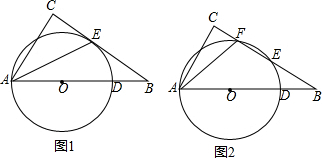
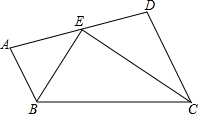 如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上.求证:BC=AB+CD.
如图所示,AB∥CD,BE,CE分别是∠ABC,∠BCD的平分线,点E在AD上.求证:BC=AB+CD.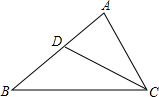 已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.
已知:BC=AC+AD,CD平分∠ACB,求证:∠A=2∠B.