题目内容
19.如图,已知△ABC中,AB=AC,∠BAC=90°,点D为BC的中点,点E、F分别在直线AB、AC上运动,且始终保持AE=CF.(1)如图①,若点E、F分别在线段AB,AC上,求证:DE=DF且DE⊥DF;
(2)如图②,若点E、F分别在线段AB,CA的延长线上,(1)中的结论是否依然成立?说明理由.
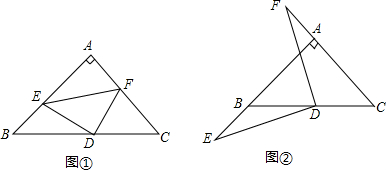
分析 (1)利用等腰直角三角形的性质得出AD=BD=DC,进而证明△AED≌△CFD,利用全等三角形的性质得出DE=DF,∠ADE=∠CDF进而得出△DEF为等腰直角三角形;
(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,首先利用已知得出AD=BD=DC,进而利用全等三角形的判定得出△AED≌△CFD.
解答 解:(1)如图①,连接AD,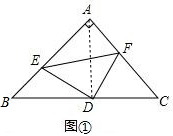
∵∠BAC=90°,AB=AC,D为BC中点,
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAD=∠DAC}\\{AD=DC}\end{array}\right.$,
∴△AED≌△CFD(SAS),
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF+∠ADF=90°,
∴∠ADE+∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF.
(2)若点E、F分别在线段AB,CA的延长线上,(1)中的结论依然成立,如图②,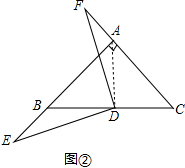
理由:∵∠BAC=90° AB=AC,D为BC中点
∴∠BAD=∠DAC=∠B=∠C=45°,
∴AD=BD=DC,
在△AED和△CFD中,
$\left\{\begin{array}{l}{AE=CF}\\{∠EAD=∠C}\\{AD=CD}\end{array}\right.$,
∴△AED≌△CFD(SAS);
∴DE=DF,∠ADE=∠CDF,
又∵∠CDF-∠ADF=90°,
∴∠ADE-∠ADF=90°,
∴∠EDF=90°,
∴DE⊥DF.
点评 此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,根据已知得出AD=BD=DC是解题关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
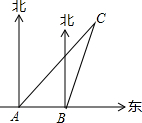 如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.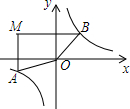 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为( )
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为( ) 如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.
如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.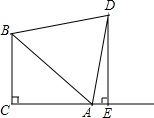 如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.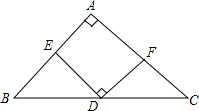 如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.
如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF. 如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.
如图,?ABED中,对角线BD平分∠ABE,过点D作DC∥AE,交BE的延长线于点C.求证:AB=CE.