题目内容
14.一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球个数是白球的3倍多10个.已知从袋中摸出一个球是红球的概率是$\frac{3}{10}$.(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走5个球(其中没有红球)求从剩余球中摸出球是红球的概率.
分析 (1)根据红、黄、白三种颜色球共有的个数乘以红球的概率即可;
(2)设白球有x个,得出黄球有(3x+10)个,根据题意列出方程,求出白球的个数,再除以总的球数即可;
(3)先求出取走5个球后,还剩的球数,再根据红球的个数,除以还剩的球数即可.
解答 解:(1)根据题意得:
100×$\frac{3}{10}$=30(个),
答:袋中红球的个数有30个.
(2)设白球有x个,则黄球有(3x+10)个,
根据题意得x+3x+10=100-30
解得x=15.
则摸出一个球是白球的概率P=$\frac{15}{100}$=$\frac{3}{20}$;
(3)因为取走5个球后,还剩95个球,其中红球的个数没有变化,
所以从剩余的球中摸出一个球是红球的概率是$\frac{30}{95}$=$\frac{6}{19}$.
点评 此题考查了概率公式:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.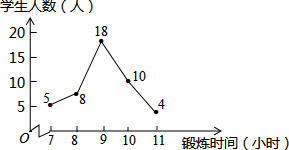 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
2.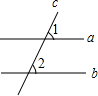 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
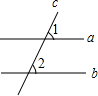 如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )
如图,直线a∥b,直线c与直线a,b都相交,∠1=60°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
9.已知一个正n边形的一个内角是它外角的5倍,则n等于( )
| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
3.学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化的试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |