题目内容
7．
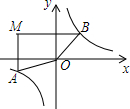如图，在平面直角坐标系中，过点M（-3，2）分别作x轴、y轴的垂线与反比例函数y=$\frac{4}{x}$的图象交于A、B两点，则四边形MAOB的面积为（ ）| A． | 6 | B． | 8 | C． | 10 | D． | 12 |
分析 根据反比例函数$y=\frac{k}{x}$中k的几何意义分别求出△AOC的面积和△OBD的面积，根据坐标特征求出四边形MCOD的面积，结合图形计算即可．
解答 解：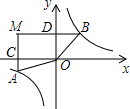
∵A、B两点在反比例函数y=$\frac{4}{x}$的图象上，
∴△AOC的面积为2，△OBD的面积为2，
∵点M（-3，2），
∴四边形MCOD的面积为6，
∴四边形MAOB的面积为6+2+2=10，
故选：C．
点评 本题考查的是反比例函数系数k的几何意义，反比例函数$y=\frac{k}{x}$中k的几何意义：图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=$\frac{1}{2}$|k|．
练习册系列答案
相关题目
2．
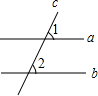如图，直线a∥b，直线c与直线a，b都相交，∠1=60°，则∠2的度数是（ ）
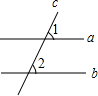如图，直线a∥b，直线c与直线a，b都相交，∠1=60°，则∠2的度数是（ ）| A． | 40° | B． | 50° | C． | 60° | D． | 70° |
3．学校组织知识竞赛，共设有20道试题，其中有关中国优秀传统文化的试题10道，实践应用试题6道，创新能力试题4道．小捷从中任选一道试题作答，他选中创新能力试题的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{10}$ | D． | $\frac{1}{5}$ |
2．国际象棋决赛在甲乙两名选手之间进行，比赛规则是：共下10局棋，每局胜方得1分，负方得0分，平局则各得0.5分，谁的积分先达到5.5分便夺冠，不继续比赛；若10局棋下完双方积分相同，则继续下，直到分出胜负为止．下完8局时，甲4胜1平．若以前8局棋取胜的频率为各自取胜的概率，那么在后面的两局棋中，甲夺冠的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{5}{8}$ | C． | $\frac{45}{64}$ | D． | $\frac{49}{64}$ |
12．在平面直角坐标系中，直线a向下平移3个单位后所得直线b经过点A（0，3），将直线b绕点A顺时针旋转60°后所得直线经过点B（-$\sqrt{3}$，0），则直线a的函数关系式为（ ）
| A． | y=-$\sqrt{3}$x | B． | y=-$\frac{\sqrt{3}}{3}$x | C． | y=-$\sqrt{3}$x+6 | D． | y=-$\frac{\sqrt{3}}{3}$x+6 |
16．
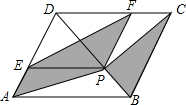如图，菱形ABCD的边长为2，较短的对角线BD的长为$\sqrt{7}$，P是BD上一点，PE∥AB，PF∥AD，分别交菱形两边于点E、F，则图中阴影部分面积为（ ）
如图，菱形ABCD的边长为2，较短的对角线BD的长为$\sqrt{7}$，P是BD上一点，PE∥AB，PF∥AD，分别交菱形两边于点E、F，则图中阴影部分面积为（ ）| A． | $\frac{3\sqrt{6}}{4}$ | B． | $\frac{3\sqrt{7}}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{3\sqrt{7}}{4}$ |
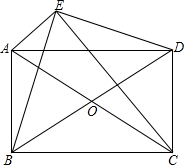如图，点E为?ABCD外一点，AE⊥EC，BE⊥ED，对角线AC，BD交于点O．