题目内容
15.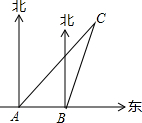 如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
如图所示,某船向正东方向航行,在A处望见某岛C在北偏东45°方向,前进6海里到达B处,测得该岛在北偏东30°方向,已知在该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁的危险?请说明理由.
分析 判断有无危险只要求出点C到AB的距离,与6海里比较大小就可以.
解答 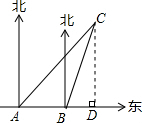 解:若该船继续向东航行,无触礁的危险.理由如下:
解:若该船继续向东航行,无触礁的危险.理由如下:
过点C作CD⊥AB于点D,
由题意得:∠CAD=45°,∠CBD=90°-30°=60°,
在Rt△CBD中,∵tan∠CBD=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan∠CBD}$=$\frac{\sqrt{3}}{3}$CD.
在等腰Rt△CBD中,CD=AD.
又∵AD-BD=6,
∴CD-$\frac{\sqrt{3}}{3}$CD=6,
解得CD=9+3$\sqrt{3}$>6,
即:若船继续向东航行,无触礁危险.
点评 本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.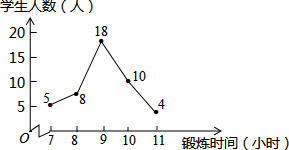 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
 某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )| A. | 18,18 | B. | 9,9 | C. | 9,10 | D. | 18,9 |
3.学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化的试题10道,实践应用试题6道,创新能力试题4道.小捷从中任选一道试题作答,他选中创新能力试题的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |
2.国际象棋决赛在甲乙两名选手之间进行,比赛规则是:共下10局棋,每局胜方得1分,负方得0分,平局则各得0.5分,谁的积分先达到5.5分便夺冠,不继续比赛;若10局棋下完双方积分相同,则继续下,直到分出胜负为止.下完8局时,甲4胜1平.若以前8局棋取胜的频率为各自取胜的概率,那么在后面的两局棋中,甲夺冠的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{45}{64}$ | D. | $\frac{49}{64}$ |
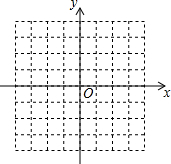
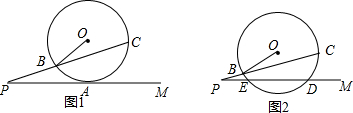
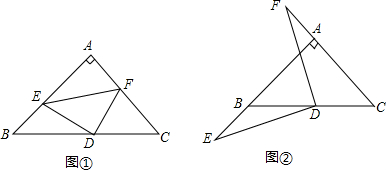
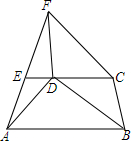 如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB.
如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB.