题目内容
4.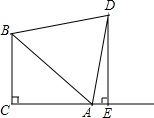 如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
如图,△ABC中,∠ACB=90°,AC=BC,D为△ABC外一点,且AD=BD,DE⊥AC交CA的延长线于E,求证:DE=AE+BC.
分析 连接CD,证明△BCD≌△ACD,得到∠BCD=∠ACD,求出∠ACD=45°,再根据DE⊥AC,得到∠CDE=∠ACD=45°,进而证明CE=DE,即可解答.
解答 解:如图,连接CD,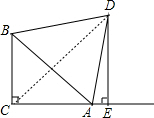
在△BCD和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{DB=AD}\\{CD=CD}\end{array}\right.$,
∴△BCD≌△ACD,
∴∠BCD=∠ACD,
∵∠ACB=90°,
∴∠ACD=$\frac{1}{2}$∠ACB=45°,
∵DE⊥AC,
∴∠CDE=∠ACD=45°,
∴CE=DE,
∴DE=AE+AC=AE+BC.
点评 本题考查了全等三角形的性质定理与判定定理、等腰三角形的性质,解决本题的关键是证明连接CD,证明△BCD≌△ACD.

练习册系列答案
相关题目
12.在平面直角坐标系中,直线a向下平移3个单位后所得直线b经过点A(0,3),将直线b绕点A顺时针旋转60°后所得直线经过点B(-$\sqrt{3}$,0),则直线a的函数关系式为( )
| A. | y=-$\sqrt{3}$x | B. | y=-$\frac{\sqrt{3}}{3}$x | C. | y=-$\sqrt{3}$x+6 | D. | y=-$\frac{\sqrt{3}}{3}$x+6 |
16. 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )| A. | $\frac{3\sqrt{6}}{4}$ | B. | $\frac{3\sqrt{7}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{7}}{4}$ |
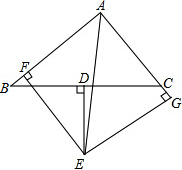 如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.
如图,△ABC中,D为BC的中点,DE⊥BC交∠BAC的平分线AE于点E,EF⊥AB于F,EG⊥AG交AC的延长线于G.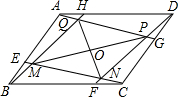 如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.
如图,在?ABCD中,AH=CF,BE=DG,连结AG,BH,CE,DF,交点分别为M,N,P,Q,若MP与NQ相交于O,求证:OM=OP,ON=OQ.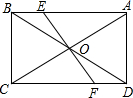 如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.
如图,已知在?ABCD中,对角线AC和BD相交于点O,EF过点O,且分别与AB,CD相交于点E、F,AB=10,BC=6,OF=3.2,求四边形AEFD的周长.