题目内容
11.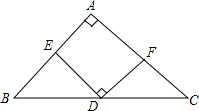 如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.
如下图,在△ABC中,AB=AC,∠BAC=90°,D是BC的中点,ED⊥FD且分别交AB、AC于E、F.求证:BE=AF.
分析 连接AD,根据等腰直角三角形的性质,可得出AD=BD=CD,AD⊥BC,∠B=∠C=∠DAC=45°,从而可证得△BDE≌△ADF,结论得证.
解答 证明:如图,连接AD,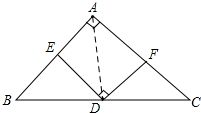
∵AB=AC,∠BAC=90°,D是BC的中点,
∴AD=BD=CD,AD⊥BC,∠B=∠C=∠DAC=45°,
∵ED⊥FD,
∴∠BDE=∠ADF,
在△BDE和△ADF中,
$\left\{\begin{array}{l}{∠EBD=∠FAD}\\{∠EDB=∠FDA}\\{BD=AD}\end{array}\right.$,
∴△BDE≌△ADF(ASA),
∴BE=AF.
点评 本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质,难度适中.“三线合一”是等腰三角形常用辅助线,要熟练掌握.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
2.国际象棋决赛在甲乙两名选手之间进行,比赛规则是:共下10局棋,每局胜方得1分,负方得0分,平局则各得0.5分,谁的积分先达到5.5分便夺冠,不继续比赛;若10局棋下完双方积分相同,则继续下,直到分出胜负为止.下完8局时,甲4胜1平.若以前8局棋取胜的频率为各自取胜的概率,那么在后面的两局棋中,甲夺冠的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{8}$ | C. | $\frac{45}{64}$ | D. | $\frac{49}{64}$ |
16.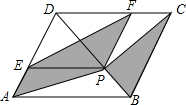 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
 如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )
如图,菱形ABCD的边长为2,较短的对角线BD的长为$\sqrt{7}$,P是BD上一点,PE∥AB,PF∥AD,分别交菱形两边于点E、F,则图中阴影部分面积为( )| A. | $\frac{3\sqrt{6}}{4}$ | B. | $\frac{3\sqrt{7}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{7}}{4}$ |
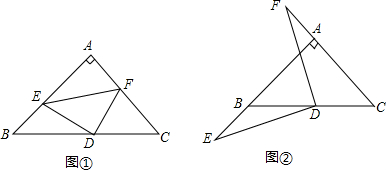
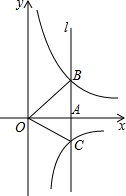 如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.
如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.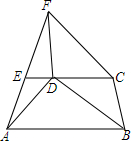 如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB.
如图.在?BCFD的对角线CD的延长线上取一点E,连接FE并延长至A点.使EA=EF,连接AB,求证:CE∥AB.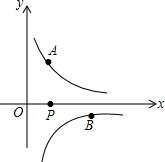 如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).
如图,已知点A($\frac{1}{2}$,y1),B(2,y2)分别为反比例函数y=$\frac{1}{x}$,y=$\frac{-1}{x}$图象上的点,动点P在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,P的坐标是($\frac{5}{2}$,0).