题目内容
19.如图,已知A、B两点在直线l的同一侧,根据题意,尺规作图.(1)在(图1)直线l上找出一点P,使PA=PB.
(2)在(图2)直线l上找出一点P,使PA+PB的值最小.
(3)在(图3)直线l上找出一点P,使PA-PB的值最大.

分析 (1)连接AB,作线段AB的垂直平分线,交直线l于点P,则点P即为所求;
(2)作B关于l的对称点B',连接AB′,线段AB′与l交于P,则P就是所求点.也可作A关于l的对称点A′;
(3)作A关于l的对称点A',直线A'B与l交于P,则P就是所求点,也可作B关于l的对称点.
解答 解:(1)如图1所示:
此时:PA=PB,
如图所示:
(2)
此时:PA+PB最小;
(3)如图所示:
此时:PA-PB最大.
点评 本题考查了轴对称-最短路线问题的应用,关键是正确画出图形,题型较好,难度适中.

练习册系列答案
相关题目
7.对一批衬衣进行抽检,统计合格衬衣的件数,得到合格衬衣的频数表如表:
估计任抽一件衬衣是合格品的概率0.95.
| 抽取件数(件) | 50 | 100 | 200 | 500 | 800 | 1000 |
| 合格频数 | 47 | 93 | 189 | 489 | 760 | 950 |
 已知:点B、E、C、F在同一直线上,AC=DF,∠A=∠D,AB∥DE.试说明:BE=CF.
已知:点B、E、C、F在同一直线上,AC=DF,∠A=∠D,AB∥DE.试说明:BE=CF.
 如图,已知在△ABC中,D为AC中点,连接BD.
如图,已知在△ABC中,D为AC中点,连接BD. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?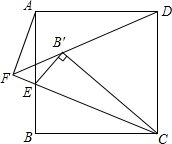 如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为$\frac{3\sqrt{10}}{5}$.
如图,E为正方形ABCD边AB上的一点,且AB=3,BE=1.将△CBE翻折得到△CB'E,连接并延长DB'与CE延长线相交于点F,连接AF,则AF的长为$\frac{3\sqrt{10}}{5}$.