题目内容
4. 如图,已知在△ABC中,D为AC中点,连接BD.
如图,已知在△ABC中,D为AC中点,连接BD.(1)若AB=10cm,BC=6cm,求中线BD的取值范围;
(2)若AB=8cm,BD=6cm,求BC的取值范围.
分析 (1)作辅助线,构建全等三角形,证明△ABD≌△CED,得CE=AB=10cm,在△BCE中,根据三边关系得:4cm<BE<16cm,则2cm<BD<8cm;
(2)同理根据三角形三边关系得:12-8<BC<12+8,即4cm<BC<20cm.
解答 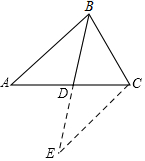 解:(1)如图,延长BD至E,使BD=DE,连接CE,
解:(1)如图,延长BD至E,使BD=DE,连接CE,
∵D为AC中点,
∴AD=DC,
在△ABD和△CED中,
∵$\left\{\begin{array}{l}{BD=DE}\\{∠ADB=∠CDE}\\{AD=CD}\end{array}\right.$,
∴△ABD≌△CED(SAS),
∴EC=AB=10,
在△BCE中,CE-BC<BE<CE+BC,
10-6<BE<10+6,
∴4<BE<16,
∴4<2BD<16,
∴2<BD<8;
则中线BD的取值范围:2cm<BD<8cm;
(2)∵AB=8,BD=6,
∴CE=AB=8,BE=2BD=12,
∴BE-EC<BC<BE+BC,
∴12-8<BC<12+8,
即4<BC<20;
则BC的取值范围:4cm<BC<20cm.
点评 本题是求三角形某边的取值范围,考查了全等三角形的判定和性质、三角形的三边关系,利用三角形全等将已知的两边和所求取值的边平移到同一三角形中,根据三边关系解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC≌△CDA,则AB与CD的位置关系是平行,若AD=3cm,AB=2cm,则四边形ABCD的周长=10cm.
如图,△ABC≌△CDA,则AB与CD的位置关系是平行,若AD=3cm,AB=2cm,则四边形ABCD的周长=10cm.
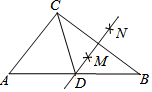 如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=8,AC=3,则△ACD的周长为11.
如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.若AB=8,AC=3,则△ACD的周长为11.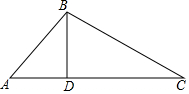 如图,在△ABC中,∠ABC=120°,BD是AC边上的高,若AB+AD=DC,则∠C等于20°.
如图,在△ABC中,∠ABC=120°,BD是AC边上的高,若AB+AD=DC,则∠C等于20°.