题目内容
8.如图1是某超市要从底楼到二楼自动扶梯设计效果图,图2是其侧面示意图.已知自动扶梯AB的长度是13m,MN是二楼楼顶,PQ是一楼地面,MN∥PQ.C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,BC为7m,在自动扶梯底端A处看C点的仰角为45°,则安装自动扶梯AB时的坡度应为多少?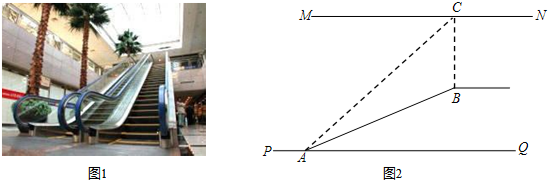
分析 延长CB交PQ于F,则CF⊥PQ,求出∠CAQ=∠ACF=45°,根据勾股定理在Rt△ABF中求出x的值.
解答  解:延长CB交PQ于F,
解:延长CB交PQ于F,
则CF⊥PQ,
∵∠CAQ=45°,
∴∠ACF=45°,
∴设AF=FC=x米,
则BF=(x-7)米,
在Rt△ABF中,
x2+(x-7)2=132,
解得x=12,
BF=12-7=5,
可得,坡度为$\frac{5}{12}$.
答:安装自动扶梯AB时的坡度应为$\frac{5}{12}$.
点评 本题考查了解直角三角形的应用--仰角俯角问题和坡度坡角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
3. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )| A. | 70° | B. | 50° | C. | 40° | D. | 80° |
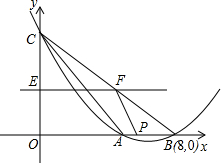 如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.
如图,抛物线y=ax2+bx+c(a>0)交x轴于A、B两点,交y轴于C点,A点在B点的左侧,已知B点坐标是(8,0),tan∠ABC=$\frac{1}{2}$,△ABC的面积为8.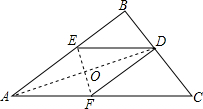 如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.
如图,在三角形纸片ABC中,∠BAC为锐角,AB=12cm,AC=15cm.按下列步骤折叠:第一次,把∠B折叠使点B落在AC边上,折痕为AD,交BC于点D;第二次折叠,使点A与点D重合,折痕分别交AB、AC于点E、F,EF与AD交于点O,展开后,连结DE、DF.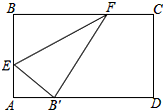 如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.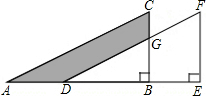 如图,将直角三角形ABC沿AB方向平移AD距离得到直角三角形DEF.已知BE=4cm,EF=7cm,CG=3cm,求图中阴影部分的面积.
如图,将直角三角形ABC沿AB方向平移AD距离得到直角三角形DEF.已知BE=4cm,EF=7cm,CG=3cm,求图中阴影部分的面积.