题目内容
18．
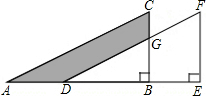如图，将直角三角形ABC沿AB方向平移AD距离得到直角三角形DEF．已知BE=4cm，EF=7cm，CG=3cm，求图中阴影部分的面积．
分析 根据平移的性质得$\frac{BG}{BC}=\frac{BD}{DE}$，得出BD=$\frac{16}{3}$，可得AB=DE=$\frac{28}{3}$，S△ABC=S△DFE，则BG=EF-CG=4，S阴影部分=S梯形DEBG，然后根据梯形的面积公式求解．
解答 解：∵直角△ABC沿CB方向平移BE的距离得到直角△DEF，
∴$\frac{BG}{BC}=\frac{BD}{DE}$，EF=BC=7，
设BD为x，可得：$\frac{x}{4+x}=\frac{4}{7}$，
解得：x=$\frac{16}{3}$，
∴AB=DE=$\frac{16}{3}+4=\frac{28}{3}$，S△ABC=S△DFE，
∴BG=EF-CG=7-3=4，
∴S阴影部分=S梯形DEBG=$\frac{1}{2}$（4+7）×4=22．
点评 本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同． ②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．
练习册系列答案
相关题目
