题目内容
16.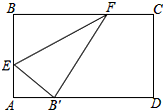 如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
如图,折叠矩形纸片ABCD,使点B落在边AD上,折痕EF的两端分别在AB、BC上(含端点),且AB=6cm,BC=10cm.求折痕EF的最大值.
分析 如图,首先运用勾股定理求出B′D的长度;再次运用勾股定理求出BE的长度,进而求出EF的长度,即可解决问题.
解答  解:如图,点F与点C重合时,折痕EF最大;
解:如图,点F与点C重合时,折痕EF最大;
由翻折的性质得,BC=B′C=10,BE=B′E;
在Rt△B′DC中,由勾股定理得:
$B'D=\sqrt{B'{C^2}-C{D^2}}=8$,
∴AB′=AD-B′D=10-8=2cm;
设BE=x,则B′E=BE=x,
AE=AB-BE=6-x,
在Rt△AB′E中,AE2+AB′2=B′E2,
即(6-x)2+22=x2,
解得$x=\frac{10}{3}$;
在Rt△BEF中,
$EF=\sqrt{B{C^2}+B{E^2}}=\sqrt{{{10}^2}+{{(\frac{10}{3})}^2}}=\frac{{10\sqrt{10}}}{3}$.
点评 该题主要考查了翻折变换的性质、勾股定理等几何知识点及其应用问题;解题的关键是首先准确判断出线段EF取最大值时,点F的位置,灵活运用翻折变换的性质、勾股定理等几何知识点来分析、判断、解答.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
11.已知方程x2+mx+n=0的两根为x1、x2(x1<x2),方程x2+mx+n-1=0的两根为x3、x4(x3<x4),则下列关系一定成立的是( )
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x4<x1<x2 | D. | x3<x1<x2<x4 |
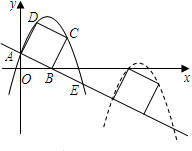 如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.
如图,已知直线y=-2x+2交坐标轴于A,B两点,以线段AB为边向上作矩形ABCD,AB:AD=1:2,过点A,D,C的抛物线与直线另一个交点为E.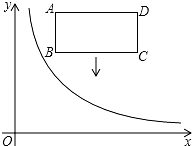 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6).将矩形ABCD向下平移,平移后的矩形记为A′B′C′D′在平移过程中,有两个顶点恰好落在反比例函数图象上. 如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.
如图,直线AB平行于CD,直线l分别于AB、CD相交于点M、N,若∠1=130°,则∠2=50°.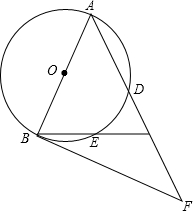 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CAB=2∠CBF.