题目内容
10.已知A、B、D三点在一条直线上,B、C、E三点在一条直线上,AB=AC,DC=DE.(1)如图1,若∠ABC=60°,求证:AD=BE;
(2)如图2,DE与AC交于点F,BE=2EC,则$\frac{DF}{EF}$=2;
(3)如图3,点D在AB的延长线上,点E在CB的延长线上,分别延长ED、AC交于点F,AB=1,∠ABC=α,$\frac{DF}{EF}$=k,求BE的长(用a、k的式子表示)

分析 (1)如图1中,作DH∥AC交BE的延长线于H.首先证明△ABC,△DBH都是等边三角形,由△DCB≌△DEH,推出BC=EH,推出BE=CH,由BD=BH,BA=BC,推出AD=CH,推出AD=BE.
(2)如图1中,作DH∥AC交BE的延长线于H.只要证明△DCB≌△DEH,可得BC=EH,推出BE=CH,由BE=2EC,推出CH=2EC,由FC∥DH,推出$\frac{DF}{EF}$=$\frac{CG}{CE}$=2.
(3)如图1中,作DH∥AC交BE于H,作AG⊥BC于G.由△DHE≌△DBC,推出EH=BC,推出EB=HC,易知BG=CG=AB•cosα=cosα,由DH∥CF,推出$\frac{CH}{CE}$=$\frac{DF}{EF}$=k,推出BE=k•CE,即BE=k•(BE+2cosα),求出BE即可.
解答 (1)证明:如图1中,作DH∥AC交BE的延长线于H.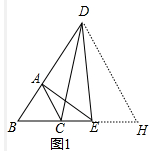
∵AB=AC,
∴∠B=∠ACB=∠H,
∴DB=DH,
∵∠B=60°,
∴△ABC,△DBH都是等边三角形,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠DCB=∠DEH,
在△DCB和△DEH中,
$\left\{\begin{array}{l}{∠B=∠H}\\{∠DCB=∠DEH}\\{DB=DH}\end{array}\right.$,
∴△DCB≌△DEH,
∴BC=EH,
∴BE=CH,
∵BD=BH,BA=BC,
∴AD=CH,
∴AD=BE.
(2)解:如图2中,作DH∥AC交BE的延长线于H.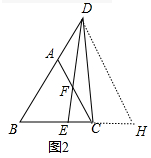
∵AB=AC,
∴∠B=∠ACB=∠H,
∴DB=DH,
∵DC=DE,
∴∠DCE=∠DEC,
∴∠DCB=∠DEH,
在△DCB和△DEH中,
$\left\{\begin{array}{l}{∠B=∠H}\\{∠DCB=∠DEH}\\{DB=DH}\end{array}\right.$,
∴△DCB≌△DEH,
∴BC=EH,
∴BE=CH,
∵BE=2EC,
∴CH=2EC,
∵FC∥DH,
∴$\frac{DF}{EF}$=$\frac{CG}{CE}$=2,
故答案为2.
(3)解:如图3中,作DH∥AC交BE于H,作AG⊥BC于G.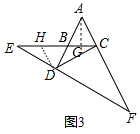
∵AB=AC,
∴∠ABC=∠ACB=∠DHC=∠DBH,
∴DH=DB,∠EHD=∠DBC,
∵DE=DC,
∴∠E=∠DCB,
在△DHE和△DBC中,
$\left\{\begin{array}{l}{∠E=∠DCB}\\{∠DHE=∠DBC}\\{DE=DC}\end{array}\right.$,
∴△DHE≌△DBC,
∴EH=BC,
∴EB=HC,
∵AB=AC,AG⊥BC,
∴BG=CG=AB•cosα=cosα,
∵DH∥CF,
∴$\frac{CH}{CE}$=$\frac{DF}{EF}$=k,
∴BE=k•CE,
∴BE=k•(BE+2cosα),
∴BE=$\frac{2kcosα}{1-k}$.
点评 本题考查三角形综合题、全等三角形的判定和性质、等边三角形的判定和性质、等腰三角形的性质、平行线分线段成比例定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 由向左平移3个单位,再向上平移2个单位 | |
| B. | 由向右平移3个单位,再向下平移2个单位 | |
| C. | 由向右平移3个单位,再向上平移2个单位 | |
| D. | 由向左平移3个单位,再向下平移2个单位 |
| A. | 2x=196+4(70-x) | B. | 4x+2(70-x)=196 | C. | 2x+4(70-x)=196 | D. | 2x+196=4(70-x) |
| A. | x=-1 | B. | x<0 | C. | x≥0 | D. | x≤0 |
| A. | x>2 | B. | x≥-2 | C. | x≤-2 | D. | x>-2 |
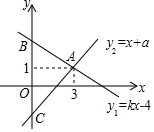 如图,一次函数y1=kx+4与y2=x+a的图象相交于点A(3,1),与y轴分别相交于点B、C两点.
如图,一次函数y1=kx+4与y2=x+a的图象相交于点A(3,1),与y轴分别相交于点B、C两点. 如图,点O是△ABC内的一点,AB=AC,∠BAC=90°,∠BOC=120°,将△AOB绕点A按逆时针方向旋转90°得到△ADC,连结OD.
如图,点O是△ABC内的一点,AB=AC,∠BAC=90°,∠BOC=120°,将△AOB绕点A按逆时针方向旋转90°得到△ADC,连结OD.