题目内容
20．
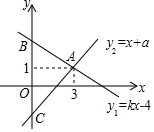如图，一次函数y1=kx+4与y2=x+a的图象相交于点A（3，1），与y轴分别相交于点B、C两点．（1）求这两个一次函数的解析式；
（2）求△ABC的面积．
分析 （1）将点A的坐标代入y1=kx+4与y2=x+a，解得k，a，再将k，a的值代入解析式可得结果；
（2）利用一次函数y1=kx+4与y2=x+a与y轴的交点，求得B、C，可得BC的长，利用三角形的面积公式可得结果．
解答 解：（1）将点A（3，1）的坐标代入y1=kx+4与y2=x+a，
得1=3k+4，1=3+a，
解得k=-1，a=-2，
∴这两个一次函数的解析式为y1=-x+4，y2=x-2；
（2）令x=0，可得y1=0+4=4，y2=0-2=-2；
∴B的坐标为（0，4）；C的坐标为（0，-2），
BC=6，
∴S△ABC=$\frac{1}{2}×6×3$=9．
点评 本题主要考查了两直线平行和相交问题，令x=0，求得与y轴的交点坐标是解答此题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
8．下列分式中，最简分式是（ ）
| A． | $\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}$ | B． | $\frac{x+1}{{x}^{2}-1}$ | ||
| C． | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | D． | $\frac{{x}^{2}-36}{2x+12}$ |
15．若分式$\frac{x+1}{x-1}$有意义，则x满足的条件是（ ）
| A． | x=1 | B． | x=-1 | C． | x≠1 | D． | x≠-1 |
如图，在△ABC中，AB=AC，BD和CE是两腰上的高，交于点O，连接AO并延长交BC于点F．则图中全等三角形的对数是（ ）
9．
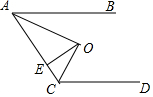如图所示，AB∥CD，O为∠BAC、∠ACD的平分线交点，OE⊥AC于E，若OE=2，则AB与CD之间的距离是（ ）
如图所示，AB∥CD，O为∠BAC、∠ACD的平分线交点，OE⊥AC于E，若OE=2，则AB与CD之间的距离是（ ）| A． | 2 | B． | 4 | C． | 8 | D． | 无法确定 |
