题目内容
2.已知等腰三角形的周长为26cm,底边长y(cm)与腰长x(cm)之间的函数关系式是y=26-2x,自变量的取值范围是$\frac{13}{2}$<x<13.分析 根据题意列出函数关系式即可;
①根据三角形的三边关系定理得出x+x>26-2x;②根据三角形的边长不能为负数和0得出y=26-2x>0,x>0,求出符合以上条件的解集即可.
解答 解:底边y与腰长x之间的函数关系式是y=26-2x;
①根据三角形的三边关系定理得:x+x>y,
即x+x>26-2x,
x>$\frac{13}{2}$,
②y=26-2x>0,x>0
解得:$\frac{13}{2}$<x<13,
即自变量x的取值范围是$\frac{13}{2}$<x<13,
故答案为:y=26-2x;$\frac{13}{2}$<x<13.
点评 本题考查了一次函数的应用和三角形的三边关系定理,关键是能根据题意得出不等式x+x>12-2x,y=12-2x>0,x>0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.绝对值相等的两数在数轴上对应两点的距离为8,则这两个数为( )
| A. | ±8 | B. | 0和-8 | C. | 0和8 | D. | 4和-4 |
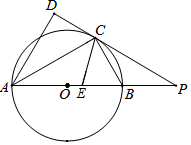 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.