题目内容
15.计算(1)计算:$\sqrt{25}$-$\root{3}{-27}$+$\sqrt{\frac{1}{4}}$-|1-$\sqrt{3}$|.
(2)求x的值:16(x+1)2=25.
(3)化简:$\frac{{x}^{2}}{x-5}$+$\frac{25}{5-x}$.
(4)化简:$\frac{{x}^{2}}{x-1}$-x-1.
分析 (1)原式利用平方根、立方根定义,以及绝对值的代数意义化简,计算即可得到结果;
(2)方程整理后,利用平方根定义开方即可求出x的值;
(3)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(4)原式通分并利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=5+3+$\frac{1}{2}$-$\sqrt{3}$+1=9$\frac{1}{2}$-$\sqrt{3}$;
(2)方程整理得:(x+1)2=$\frac{25}{16}$,
开方得:x+1=±$\frac{5}{4}$,
解得:x=$\frac{1}{4}$或x=-$\frac{9}{4}$;
(3)原式=$\frac{{x}^{2}-25}{x-5}$=$\frac{(x+5)(x-5)}{x-5}$=x+5;
(4)原式=$\frac{{x}^{2}-(x+1)(x-1)}{x-1}$=$\frac{1}{x-1}$.
点评 此题考查了分式的加减法,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )
 有理数a、b在数轴上的位置如图所示,则正确的式子是( )
有理数a、b在数轴上的位置如图所示,则正确的式子是( )| A. | a>b | B. | a>-b | C. | -a<-b | D. | a<b |
20. 如图,∠AOB为平角,且∠AOC=$\frac{2}{7}$∠BOC,则∠BOC的度数是( )
如图,∠AOB为平角,且∠AOC=$\frac{2}{7}$∠BOC,则∠BOC的度数是( )
 如图,∠AOB为平角,且∠AOC=$\frac{2}{7}$∠BOC,则∠BOC的度数是( )
如图,∠AOB为平角,且∠AOC=$\frac{2}{7}$∠BOC,则∠BOC的度数是( )| A. | 140° | B. | 135° | C. | 120° | D. | 40° |
7.绝对值相等的两数在数轴上对应两点的距离为8,则这两个数为( )
| A. | ±8 | B. | 0和-8 | C. | 0和8 | D. | 4和-4 |
 如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
如图,在△ABC中,AB=AC,BD和CE是两腰上的高,交于点O,连接AO并延长交BC于点F.则图中全等三角形的对数是( )
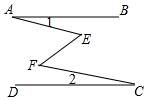 已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.
已知AB∥CD,∠AEF=∠EFC,探究:∠1与∠2的大小关系,并说明道理.