题目内容
13.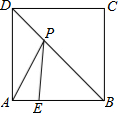 如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)
如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)
分析 连接EC交BD于点P,此时PA+PE最小,在RT△EBC中求出EC即可解决问题.
解答 解: 连接EC交BD于点P,此时PA+PE最小.
连接EC交BD于点P,此时PA+PE最小.
理由:∵四边形ABCD是正方形,
∴A、C关于直线BD对称,
∴PA+PE=PC+PE=EC,
∴此时PA+PE最小(两点之间线段最短),
PA+PE最小值=EC=$\sqrt{B{C}^{2}+E{B}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5.
故答案为5.
点评 本题考查矩形的性质、轴对称-最短问题、勾股定理等知识,解题的关键是理由轴对称的性质正确找到点P的位置,属于中考常考题型.

练习册系列答案
相关题目
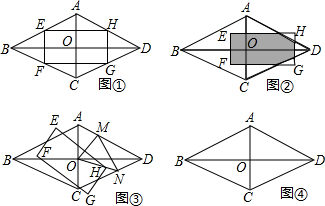
2.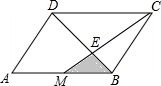 如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )
如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )
 如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )
如图,已知M是?ABCD的AB边的中点,CM交BD于E,则图中阴影部分的面积与?ABCD的面积之比是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
3.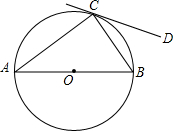 如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
 如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )
如图,点C是⊙O上的一点,AB是⊙O的直径,∠CAB=∠DCB,那么CD与⊙O的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相交或相切 |
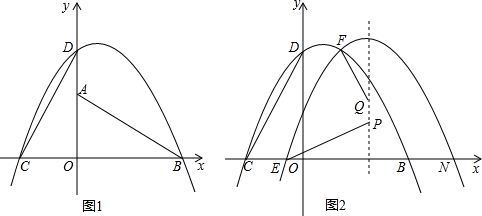
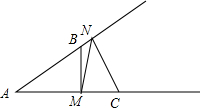 已知∠BAC=30°,AB=3,AC=4,M在AC上,N在AB上,则BM+MN+NC的最小值是$\frac{3}{2}$+2$\sqrt{3}$.
已知∠BAC=30°,AB=3,AC=4,M在AC上,N在AB上,则BM+MN+NC的最小值是$\frac{3}{2}$+2$\sqrt{3}$.