题目内容
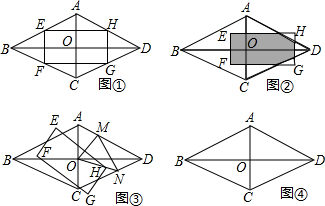
4.如图①,菱形ABCD中,对角线AC、BD相交于点O,AB=5,AC=2$\sqrt{5}$,E、F、G、H分别为菱形的四边中点,顺次连接E、F、G、H四点得矩形EFGH.(1)求矩形EFGH的边EF、EH的长;
(2)如图②,固定菱形ABCD,将矩形EFGH沿OD方向向右平移,直至点D落在EF上时停止运动.设平移距离为x,记矩形EFGH与菱形ABCD重叠部分的面积为S,求S与x之间的函数关系式,并指出x的取值范围;
(3)如图③,固定菱形ABCD,将矩形EFGH绕点O旋转,使边EH的中垂线OM交线段AD于点M,射线OH交线段CD于点N,连接MN.当△MDN为直角三角形时,请直接写出AM的长.
分析 (1)由菱形的性质得到得到直角三角形,再由直角三角形斜边的中线等于斜边的一半;
(2)由菱形的性质和矩形的性质,分段表示出线段,求出三角形的面积;
(3)根据△AOM∽△CON得到AM与CN的关系,再分∠MND和∠NMD为直角计算即可.
解答 解:(1)∵EF是△ABC的中位线,
∴EF=$\frac{1}{2}$AC=$\sqrt{5}$,
∵菱形ABCD中,AC⊥BD,AO=$\frac{1}{2}$AC=$\sqrt{5}$,
∴在Rt△ABO中,BO=$\sqrt{{5}^{2}+(\sqrt{5})^{2}}$=2$\sqrt{5}$,
∴BD=4$\sqrt{5}$,
∵EH是△ABD的中位线,
∴EH=$\frac{1}{2}$BD=2$\sqrt{5}$,
(2)如图1,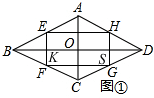
设EF,HG分别交BD于点K,S,
∴BK=KO=OS=SD=$\sqrt{5}$,
∴当点D在HG上时,x=$\sqrt{5}$,
当点E在AD上时,x=2$\sqrt{5}$,
当点D在EF上时,x=3$\sqrt{5}$,
Ⅰ、当0≤x≤$\sqrt{5}$时,如图2,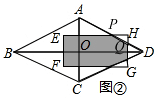
设EH,HG分别交AD,于P.Q两点,
∴PH=x,HQ=$\frac{1}{2}$x,
∴S△PHG=$\frac{1}{4}$x2,
由对称性知,S=S矩形EFGH-2S△PHG=$\sqrt{5}$×$\sqrt{5}$-2×$\frac{1}{2}$x2=-$\frac{1}{2}$x2+10;
Ⅱ、当$\sqrt{5}$≤x≤2$\sqrt{5}$,如图5,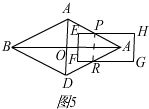
设FG交AD于P,
∴EP=2$\sqrt{5}$-x,
∴S矩形EFRP=(2$\sqrt{5}$-x)×$\sqrt{5}$=10-$\sqrt{5}$x,
∵△PRD与图1中的△DHG的面积相等,
∴S△PRD=$\frac{1}{2}$×$\sqrt{5}$×$\sqrt{5}$=$\frac{5}{2}$,
∴S=S矩形EFRP+S△PRD=10-$\sqrt{5}$x+$\frac{5}{2}$=-$\sqrt{5}$x+$\frac{25}{2}$,
Ⅲ、当2$\sqrt{5}$≤x≤3$\sqrt{5}$时,如图6,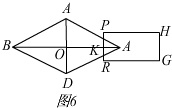
设EF交OD于K,
∴DK=3$\sqrt{5}$-x,
∴S=$\frac{1}{2}$(3$\sqrt{5}$-x)(3$\sqrt{5}$-x)=$\frac{1}{2}$(3$\sqrt{5}$-x)2;
(3)如图7,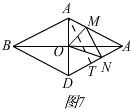
由题知,∠MON=∠OAD,
∵∠MON+∠CON=∠OAD+∠AMO,
∴∠CON=∠AMO,
∵∠OAD=∠ACD,
∴△AOM∽△CON,
设AM=a,CN=b,
∴$\frac{a}{\sqrt{5}}=\frac{\sqrt{5}}{b}$,
∴b=$\frac{5}{a}$,
∴DM=5-a,DN=5-$\frac{5}{a}$,
过A点作AT⊥CD,
∴S△ACD=$\frac{1}{2}$×5×AT=$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{5}$,
∴AT=4,
∵DT=3,
∴cos∠ADC=$\frac{3}{5}$,
Ⅰ、若∠MNO=90°,
∴cos∠ADC=$\frac{DN}{DM}=\frac{3}{5}$,
∴$\frac{5-\frac{5}{a}}{5-a}=\frac{3}{5}$,
∴a1=$\frac{5}{3}$,a2=-5(舍),
Ⅱ、若∠NMO=90°,
∴cos∠ADC=$\frac{DM}{DN}=\frac{3}{5}$,
∴$\frac{5-a}{5-\frac{5}{a}}=\frac{3}{5}$,
∴a1=3,a2=-1(舍),
点评 此题是几何变换综合题,主要考查了菱形的性质,矩形的性质,相似三角形的判定和性质,锐角三角函数,解本题的关键是运动过程中,分段用运动时间表示线段,也是解本题的难点.

| A. | 2tan60° | B. | $\sqrt{8}$ | C. | $\root{3}{16}$ | D. | π |
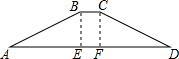 如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,为消除淮河灾害,某市水利部门修建了横断面是梯形的淮河大坝,坝顶宽6米,坝高BE=CF=20米,斜坡AB的坡角∠A=30°,斜坡CD的坡度i=1:3,(坡度是指坡面的铅直高度与水平宽度的比).求坝底AD的宽.(结果保留整数,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
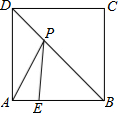 如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)
如图,E为正方形ABCD边AB上一点,BE=3,AE=1,P为对角线BD上一个动点,则PA+PE的最小值是5(正方形的四条边相等,四个角是直角)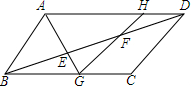 如图,E,F是平行四边形ABCD的对角线AC上的三等分点,连接AE并延长,交BC于点G,连接GF并延长,交AD于点H,若AD=12,求DH的长.
如图,E,F是平行四边形ABCD的对角线AC上的三等分点,连接AE并延长,交BC于点G,连接GF并延长,交AD于点H,若AD=12,求DH的长.